Kombinationen zurückgeben
Wählen Sie unter Verwendung einer Zahlentabelle oder eines Zahlengenerierungs-CTE 0 bis 2^n - 1 aus. Verwenden Sie die Bitpositionen, die Einsen in diesen Zahlen enthalten, um das Vorhandensein oder Fehlen der relativen Mitglieder in der Kombination anzuzeigen, und eliminieren Sie diejenigen, die keine haben die richtige Anzahl von Werten haben, sollten Sie in der Lage sein, eine Ergebnismenge mit allen gewünschten Kombinationen zurückzugeben.
WITH Nums (Num) AS (
SELECT Num
FROM Numbers
WHERE Num BETWEEN 0 AND POWER(2, @n) - 1
), BaseSet AS (
SELECT ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), *
FROM @set
), Combos AS (
SELECT
ComboID = N.Num,
S.Value,
Cnt = Count(*) OVER (PARTITION BY N.Num)
FROM
Nums N
INNER JOIN BaseSet S ON N.Num & S.ind <> 0
)
SELECT
ComboID,
Value
FROM Combos
WHERE Cnt = @k
ORDER BY ComboID, Value;
Diese Abfrage funktioniert ziemlich gut, aber ich dachte an eine Möglichkeit, sie zu optimieren, indem ich aus den Nifty Parallel Bit Count um zuerst die richtige Anzahl von Artikeln auf einmal zu erhalten. Dies ist 3- bis 3,5-mal schneller (sowohl CPU als auch Zeit):
WITH Nums AS (
SELECT Num, P1 = (Num & 0x55555555) + ((Num / 2) & 0x55555555)
FROM dbo.Numbers
WHERE Num BETWEEN 0 AND POWER(2, @n) - 1
), Nums2 AS (
SELECT Num, P2 = (P1 & 0x33333333) + ((P1 / 4) & 0x33333333)
FROM Nums
), Nums3 AS (
SELECT Num, P3 = (P2 & 0x0f0f0f0f) + ((P2 / 16) & 0x0f0f0f0f)
FROM Nums2
), BaseSet AS (
SELECT ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), *
FROM @set
)
SELECT
ComboID = N.Num,
S.Value
FROM
Nums3 N
INNER JOIN BaseSet S ON N.Num & S.ind <> 0
WHERE P3 % 255 = @k
ORDER BY ComboID, Value;
Ich ging und las die Bit-Zählseite und denke, dass dies besser funktionieren könnte, wenn ich nicht die % 255 mache, sondern den ganzen Weg mit Bit-Arithmetik gehe. Bei Gelegenheit werde ich das ausprobieren und sehen, wie es sich bewährt.
Meine Leistungsansprüche basieren auf Abfragen, die ohne die ORDER BY-Klausel ausgeführt werden. Zur Verdeutlichung zählt dieser Code die Anzahl der gesetzten 1-Bits in Num aus den Numbers Tisch. Das liegt daran, dass die Zahl als eine Art Indexer verwendet wird, um auszuwählen, welche Elemente der Menge in der aktuellen Kombination enthalten sind, sodass die Anzahl der 1-Bits gleich bleibt.
Ich hoffe es gefällt euch!
Fürs Protokoll, diese Technik, bei der das Bitmuster von ganzen Zahlen verwendet wird, um Mitglieder einer Menge auszuwählen, habe ich als "Vertical Cross Join" bezeichnet. Dies führt effektiv zu einer Kreuzverknüpfung mehrerer Datensätze, wobei die Anzahl der Sätze und Kreuzverknüpfungen beliebig ist. Hier ist die Anzahl der Sätze die Anzahl der gleichzeitig entnommenen Elemente.
Eigentlich würde Cross Joining im üblichen horizontalen Sinne (das Hinzufügen weiterer Spalten zur bestehenden Spaltenliste mit jedem Join) etwa so aussehen:
SELECT
A.Value,
B.Value,
C.Value
FROM
@Set A
CROSS JOIN @Set B
CROSS JOIN @Set C
WHERE
A.Value = 'A'
AND B.Value = 'B'
AND C.Value = 'C'
Meine obigen Abfragen "kreuzen" so oft wie nötig mit nur einem Join. Die Ergebnisse sind im Vergleich zu tatsächlichen Cross-Joins zwar unpivotiert, aber das ist Nebensache.
Kritik Ihres Kodex
Darf ich zunächst diese Änderung an Ihrer Fakultäts-UDF vorschlagen:
ALTER FUNCTION dbo.Factorial (
@x bigint
)
RETURNS bigint
AS
BEGIN
IF @x <= 1 RETURN 1
RETURN @x * dbo.Factorial(@x - 1)
END
Jetzt können Sie viel größere Kombinationen berechnen und es ist effizienter. Sie könnten sogar die Verwendung von decimal(38, 0) in Betracht ziehen größere Zwischenrechnungen in Ihren Kombinationsrechnungen zu ermöglichen.
Zweitens gibt Ihre angegebene Abfrage nicht die richtigen Ergebnisse zurück. Wenn Sie beispielsweise meine Testdaten aus den folgenden Leistungstests verwenden, ist Satz 1 identisch mit Satz 18. Es sieht so aus, als würde Ihre Abfrage einen Gleitstreifen verwenden, der sich umschließt:Jeder Satz besteht immer aus 5 benachbarten Mitgliedern und sieht ungefähr so aus (ich drehte mich um es besser sichtbar zu machen):
1 ABCDE
2 ABCD Q
3 ABC PQ
4 AB OPQ
5 A NOPQ
6 MNOPQ
7 LMNOP
8 KLMNO
9 JKLMN
10 IJKLM
11 HIJKL
12 GHIJK
13 FGHIJ
14 EFGHI
15 DEFGH
16 CDEFG
17 BCDEF
18 ABCDE
19 ABCD Q
Vergleichen Sie das Muster aus meinen Abfragen:
31 ABCDE
47 ABCD F
55 ABC EF
59 AB DEF
61 A CDEF
62 BCDEF
79 ABCD G
87 ABC E G
91 AB DE G
93 A CDE G
94 BCDE G
103 ABC FG
107 AB D FG
109 A CD FG
110 BCD FG
115 AB EFG
117 A C EFG
118 BC EFG
121 A DEFG
...
Nur um das Bitmuster -> Index der Kombination für alle Interessierten nach Hause zu bringen, beachten Sie, dass 31 in Binär =11111 und das Muster ABCDE ist. 121 in Binärform ist 1111001 und das Muster ist A__DEFG (rückwärts abgebildet).
Leistungsergebnisse mit einer Tabelle mit reellen Zahlen
Ich habe bei meiner zweiten Abfrage oben einige Leistungstests mit großen Sätzen durchgeführt. Ich habe derzeit keine Aufzeichnungen über die verwendete Serverversion. Hier sind meine Testdaten:
DECLARE
@k int,
@n int;
DECLARE @set TABLE (value varchar(24));
INSERT @set VALUES ('A'),('B'),('C'),('D'),('E'),('F'),('G'),('H'),('I'),('J'),('K'),('L'),('M'),('N'),('O'),('P'),('Q');
SET @n = @@RowCount;
SET @k = 5;
DECLARE @combinations bigint = dbo.Factorial(@n) / (dbo.Factorial(@k) * dbo.Factorial(@n - @k));
SELECT CAST(@combinations as varchar(max)) + ' combinations', MaxNumUsedFromNumbersTable = POWER(2, @n);
Peter zeigte, dass dieser "vertikale Cross Join" nicht so gut funktioniert wie das einfache Schreiben von dynamischem SQL, um die CROSS JOINs, die er vermeidet, tatsächlich auszuführen. Für den trivialen Preis von ein paar weiteren Lesevorgängen hat seine Lösung 10- bis 17-mal bessere Metriken. Die Leistung seiner Abfrage nimmt mit zunehmendem Arbeitsaufwand schneller ab als meine, aber nicht schnell genug, um jemanden an der Verwendung zu hindern.
Der zweite Zahlensatz unten ist der Faktor, dividiert durch die erste Zeile in der Tabelle, nur um zu zeigen, wie er skaliert.
Erik
Items CPU Writes Reads Duration | CPU Writes Reads Duration
----- ------ ------ ------- -------- | ----- ------ ------ --------
17•5 7344 0 3861 8531 |
18•9 17141 0 7748 18536 | 2.3 2.0 2.2
20•10 76657 0 34078 84614 | 10.4 8.8 9.9
21•11 163859 0 73426 176969 | 22.3 19.0 20.7
21•20 142172 0 71198 154441 | 19.4 18.4 18.1
Peter
Items CPU Writes Reads Duration | CPU Writes Reads Duration
----- ------ ------ ------- -------- | ----- ------ ------ --------
17•5 422 70 10263 794 |
18•9 6046 980 219180 11148 | 14.3 14.0 21.4 14.0
20•10 24422 4126 901172 46106 | 57.9 58.9 87.8 58.1
21•11 58266 8560 2295116 104210 | 138.1 122.3 223.6 131.3
21•20 51391 5 6291273 55169 | 121.8 0.1 613.0 69.5
Extrapolierend wird meine Abfrage schließlich billiger sein (obwohl sie von Anfang an in Lesevorgängen enthalten ist), aber nicht für lange Zeit. Um 21 Artikel im Set zu verwenden, ist bereits eine Zahlentabelle erforderlich, die bis 2097152 reicht ...
Hier ist ein Kommentar, den ich ursprünglich gemacht habe, bevor mir klar wurde, dass meine Lösung mit einer spontanen Zahlentabelle drastisch besser abschneiden würde:
Leistungsergebnisse mit einer On-The-Fly-Zahlentabelle
Als ich diese Antwort ursprünglich schrieb, sagte ich:
Nun, ich habe es versucht, und das Ergebnis war, dass es viel besser funktionierte! Hier ist die Abfrage, die ich verwendet habe:
DECLARE @N int = 16, @K int = 12;
CREATE TABLE #Set (Value char(1) PRIMARY KEY CLUSTERED);
CREATE TABLE #Items (Num int);
INSERT #Items VALUES (@K);
INSERT #Set
SELECT TOP (@N) V
FROM
(VALUES ('A'),('B'),('C'),('D'),('E'),('F'),('G'),('H'),('I'),('J'),('K'),('L'),('M'),('N'),('O'),('P'),('Q'),('R'),('S'),('T'),('U'),('V'),('W'),('X'),('Y'),('Z')) X (V);
GO
DECLARE
@N int = (SELECT Count(*) FROM #Set),
@K int = (SELECT TOP 1 Num FROM #Items);
DECLARE @combination int, @value char(1);
WITH L0 AS (SELECT 1 N UNION ALL SELECT 1),
L1 AS (SELECT 1 N FROM L0, L0 B),
L2 AS (SELECT 1 N FROM L1, L1 B),
L3 AS (SELECT 1 N FROM L2, L2 B),
L4 AS (SELECT 1 N FROM L3, L3 B),
L5 AS (SELECT 1 N FROM L4, L4 B),
Nums AS (SELECT Row_Number() OVER(ORDER BY (SELECT 1)) Num FROM L5),
Nums1 AS (
SELECT Num, P1 = (Num & 0x55555555) + ((Num / 2) & 0x55555555)
FROM Nums
WHERE Num BETWEEN 0 AND Power(2, @N) - 1
), Nums2 AS (
SELECT Num, P2 = (P1 & 0x33333333) + ((P1 / 4) & 0x33333333)
FROM Nums1
), Nums3 AS (
SELECT Num, P3 = (P2 & 0x0F0F0F0F) + ((P2 / 16) & 0x0F0F0F0F)
FROM Nums2
), BaseSet AS (
SELECT Ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), *
FROM #Set
)
SELECT
@Combination = N.Num,
@Value = S.Value
FROM
Nums3 N
INNER JOIN BaseSet S
ON N.Num & S.Ind <> 0
WHERE P3 % 255 = @K;
Beachten Sie, dass ich die Werte in Variablen ausgewählt habe, um die Zeit und den Speicher zu reduzieren, die zum Testen von allem benötigt werden. Der Server macht immer noch die gleiche Arbeit. Ich habe Peters Version so modifiziert, dass sie ähnlich ist, und unnötige Extras entfernt, damit sie beide so schlank wie möglich sind. Die für diese Tests verwendete Serverversion ist Microsoft SQL Server 2008 (RTM) - 10.0.1600.22 (Intel X86) Standard Edition on Windows NT 5.2 <X86> (Build 3790: Service Pack 2) (VM) läuft auf einer VM.
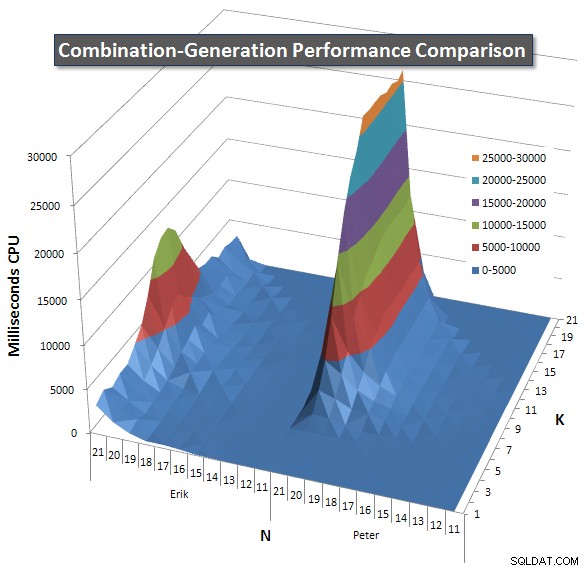
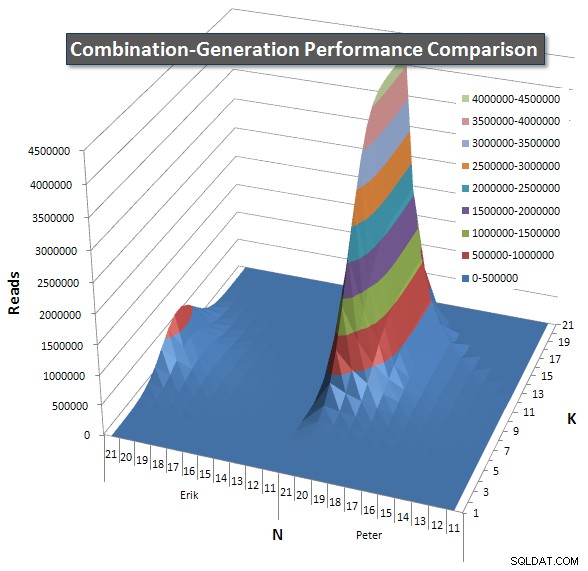
Unten sind Diagramme, die die Leistungskurven für Werte von N und K bis zu 21 zeigen. Die Basisdaten dafür sind in eine weitere Antwort auf dieser Seite . Die Werte sind das Ergebnis von 5 Durchläufen jeder Abfrage bei jedem K- und N-Wert, gefolgt vom Verwerfen der besten und schlechtesten Werte für jede Metrik und Mittelwertbildung der verbleibenden 3.
Grundsätzlich hat meine Version eine "Schulter" (in der linken Ecke des Diagramms) bei hohen Werten von N und niedrigen Werten von K, wodurch sie dort schlechter abschneidet als die dynamische SQL-Version. Dies bleibt jedoch ziemlich niedrig und konstant, und die zentrale Spitze um N =21 und K =11 ist viel niedriger für Dauer, CPU und Lesevorgänge als die dynamische SQL-Version.
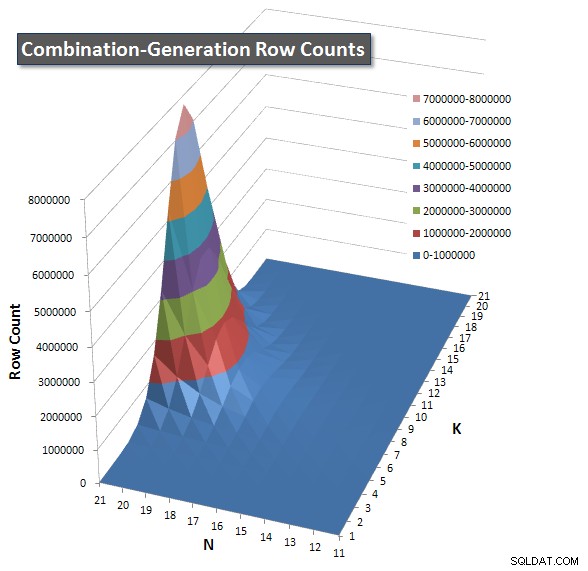
Ich habe ein Diagramm mit der Anzahl der Zeilen eingefügt, die jedes Element voraussichtlich zurückgeben wird, damit Sie sehen können, wie die Abfrage im Vergleich zur großen Aufgabe, die sie erledigen muss, abschneidet.
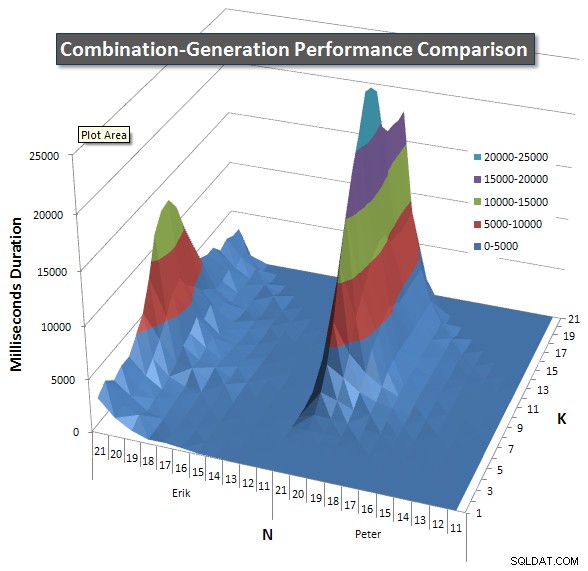
Bitte lesen Sie meine zusätzliche Antwort auf dieser Seite für die vollständigen Leistungsergebnisse. Ich habe die Zeichenbegrenzung für den Beitrag erreicht und konnte ihn hier nicht einfügen. (Irgendwelche Ideen, wo ich es sonst hinstellen könnte?) Um die Dinge im Vergleich zu den Leistungsergebnissen meiner ersten Version ins rechte Licht zu rücken, hier ist das gleiche Format wie zuvor:
Erik
Items CPU Duration Reads Writes | CPU Duration Reads
----- ----- -------- ------- ------ | ----- -------- -------
17•5 354 378 12382 0 |
18•9 1849 1893 97246 0 | 5.2 5.0 7.9
20•10 7119 7357 369518 0 | 20.1 19.5 29.8
21•11 13531 13807 705438 0 | 38.2 36.5 57.0
21•20 3234 3295 48 0 | 9.1 8.7 0.0
Peter
Items CPU Duration Reads Writes | CPU Duration Reads
----- ----- -------- ------- ------ | ----- -------- -------
17•5 41 45 6433 0 |
18•9 2051 1522 214021 0 | 50.0 33.8 33.3
20•10 8271 6685 864455 0 | 201.7 148.6 134.4
21•11 18823 15502 2097909 0 | 459.1 344.5 326.1
21•20 25688 17653 4195863 0 | 626.5 392.3 652.2
Schlussfolgerungen
- Fliegende Zahlentabellen sind besser als eine echte Tabelle, die Zeilen enthält, da das Lesen einer solchen mit einer großen Anzahl von Zeilen viel I/O erfordert. Es ist besser, ein wenig CPU zu verwenden.
- Meine anfänglichen Tests waren nicht umfassend genug, um die Leistungsmerkmale der beiden Versionen wirklich zu zeigen.
- Peters Version könnte verbessert werden, indem jeder JOIN nicht nur größer als das vorherige Element gemacht wird, sondern auch den maximalen Wert beschränkt, basierend darauf, wie viele weitere Elemente in den Satz passen müssen. Zum Beispiel gibt es bei 21 Elementen, die jeweils 21 genommen werden, nur eine Antwort von 21 Zeilen (alle 21 Elemente, einmal), aber die Zwischen-Rowsets in der dynamischen SQL-Version, früh im Ausführungsplan, enthalten Kombinationen wie " AU" in Schritt 2, obwohl dies beim nächsten Join verworfen wird, da kein höherer Wert als "U" verfügbar ist. In ähnlicher Weise enthält ein Zwischen-Rowset bei Schritt 5 "ARSTU", aber die einzig gültige Kombination an diesem Punkt ist "ABCDE". Diese verbesserte Version hätte keine niedrigere Spitze in der Mitte, was sie möglicherweise nicht genug verbessern würde, um der klare Gewinner zu werden, aber sie würde zumindest symmetrisch werden, sodass die Diagramme nicht über die Mitte der Region hinaus auf Maximum bleiben würden, sondern zurückfallen würden auf nahe 0, wie es meine Version tut (siehe die obere Ecke der Spitzen für jede Abfrage).
Daueranalyse
- Es gibt keinen wirklich signifikanten Unterschied zwischen den Versionen in der Dauer (> 100 ms) bis 14 Elemente, die jeweils 12 gleichzeitig aufgenommen wurden. Bis zu diesem Zeitpunkt gewinnt meine Version 30 Mal und die dynamische SQL-Version 43 Mal.
- Ab 14•12 war meine Version 65-mal schneller (59>100ms), die dynamische SQL-Version 64mal schneller (60>100ms). Immer wenn meine Version schneller war, sparte sie jedoch eine durchschnittliche Gesamtdauer von 256,5 Sekunden ein, und wenn die dynamische SQL-Version schneller war, sparte sie 80,2 Sekunden ein.
- Die durchschnittliche Gesamtdauer für alle Versuche betrug Erik 270,3 Sekunden, Peter 446,2 Sekunden.
- Wenn eine Nachschlagetabelle erstellt würde, um zu bestimmen, welche Version verwendet werden soll (die schnellere für die Eingaben auswählen), könnten alle Ergebnisse in 188,7 Sekunden ausgeführt werden. Die Verwendung des langsamsten würde jedes Mal 527,7 Sekunden dauern.
Leseanalyse
Die Daueranalyse zeigte, dass meine Abfrage mit einem erheblichen, aber nicht übermäßig großen Betrag gewann. Wenn die Metrik auf Reads umgestellt wird, ergibt sich ein ganz anderes Bild – meine Abfrage verwendet im Durchschnitt 1/10 der Reads.
- Es gibt keinen wirklich signifikanten Unterschied zwischen den Versionen in Lesevorgängen (>1000) bis 9 Elemente, die 9 gleichzeitig genommen werden. Bis zu diesem Punkt gewinnt meine Version 30 Mal und die dynamische SQL-Version 17 Mal.
- Beginnend bei 9•9 verwendete meine Version 118 Mal weniger Lesevorgänge (113>1000), die dynamische SQL-Version 69 Mal (31>1000). Immer wenn meine Version jedoch weniger Lesevorgänge benötigte, sparte sie insgesamt durchschnittlich 75,9 Millionen Lesevorgänge ein, und wenn die dynamische SQL-Version schneller war, sparte sie 380.000 Lesevorgänge ein.
- Die gesamten durchschnittlichen Reads für alle Studien betrugen Erik 8,4 Mio., Peter 84 Mio.
- Wenn eine Nachschlagetabelle erstellt würde, um zu bestimmen, welche Version verwendet werden soll (Auswahl der besten Version für die Eingaben), könnten alle Ergebnisse in 8 Millionen Lesevorgängen durchgeführt werden. Die Verwendung des schlechtesten würde jedes Mal 84,3 Millionen Lesevorgänge erfordern.
Ich wäre sehr daran interessiert, die Ergebnisse einer aktualisierten dynamischen SQL-Version zu sehen, die die zusätzliche Obergrenze für die in jedem Schritt ausgewählten Elemente setzt, wie ich oben beschrieben habe.
Nachtrag
Die folgende Version meiner Abfrage erzielt eine Verbesserung von etwa 2,25 % gegenüber den oben aufgeführten Leistungsergebnissen. Ich habe die HAKMEM-Bitzählmethode des MIT verwendet und ein Convert(int) hinzugefügt auf das Ergebnis von row_number() da es einen Bigint zurückgibt. Natürlich wünschte ich, dies wäre die Version, die ich für alle oben genannten Leistungstests und Diagramme und Daten verwendet hätte, aber es ist unwahrscheinlich, dass ich sie jemals wiederholen werde, da sie arbeitsintensiv war.
WITH L0 AS (SELECT 1 N UNION ALL SELECT 1),
L1 AS (SELECT 1 N FROM L0, L0 B),
L2 AS (SELECT 1 N FROM L1, L1 B),
L3 AS (SELECT 1 N FROM L2, L2 B),
L4 AS (SELECT 1 N FROM L3, L3 B),
L5 AS (SELECT 1 N FROM L4, L4 B),
Nums AS (SELECT Row_Number() OVER(ORDER BY (SELECT 1)) Num FROM L5),
Nums1 AS (
SELECT Convert(int, Num) Num
FROM Nums
WHERE Num BETWEEN 1 AND Power(2, @N) - 1
), Nums2 AS (
SELECT
Num,
P1 = Num - ((Num / 2) & 0xDB6DB6DB) - ((Num / 4) & 0x49249249)
FROM Nums1
),
Nums3 AS (SELECT Num, Bits = ((P1 + P1 / 8) & 0xC71C71C7) % 63 FROM Nums2),
BaseSet AS (SELECT Ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), * FROM #Set)
SELECT
N.Num,
S.Value
FROM
Nums3 N
INNER JOIN BaseSet S
ON N.Num & S.Ind <> 0
WHERE
Bits = @K
Und ich konnte nicht widerstehen, eine weitere Version zu zeigen, die eine Suche durchführt, um die Anzahl der Bits zu erhalten. Es kann sogar schneller sein als andere Versionen:
DECLARE @BitCounts binary(255) =
0x01010201020203010202030203030401020203020303040203030403040405
+ 0x0102020302030304020303040304040502030304030404050304040504050506
+ 0x0102020302030304020303040304040502030304030404050304040504050506
+ 0x0203030403040405030404050405050603040405040505060405050605060607
+ 0x0102020302030304020303040304040502030304030404050304040504050506
+ 0x0203030403040405030404050405050603040405040505060405050605060607
+ 0x0203030403040405030404050405050603040405040505060405050605060607
+ 0x0304040504050506040505060506060704050506050606070506060706070708;
WITH L0 AS (SELECT 1 N UNION ALL SELECT 1),
L1 AS (SELECT 1 N FROM L0, L0 B),
L2 AS (SELECT 1 N FROM L1, L1 B),
L3 AS (SELECT 1 N FROM L2, L2 B),
L4 AS (SELECT 1 N FROM L3, L3 B),
L5 AS (SELECT 1 N FROM L4, L4 B),
Nums AS (SELECT Row_Number() OVER(ORDER BY (SELECT 1)) Num FROM L5),
Nums1 AS (SELECT Convert(int, Num) Num FROM Nums WHERE Num BETWEEN 1 AND Power(2, @N) - 1),
BaseSet AS (SELECT Ind = Power(2, Row_Number() OVER (ORDER BY Value) - 1), * FROM ComboSet)
SELECT
@Combination = N.Num,
@Value = S.Value
FROM
Nums1 N
INNER JOIN BaseSet S
ON N.Num & S.Ind <> 0
WHERE
@K =
Convert(int, Substring(@BitCounts, N.Num & 0xFF, 1))
+ Convert(int, Substring(@BitCounts, N.Num / 256 & 0xFF, 1))
+ Convert(int, Substring(@BitCounts, N.Num / 65536 & 0xFF, 1))
+ Convert(int, Substring(@BitCounts, N.Num / 16777216, 1))