Wenn Sie nach einem Approximationsalgorithmus suchen, schlage ich vor, nach einem k-Means-Algorithmus oder einem hierarchischen Cluster zu suchen, insbesondere nach einer Monsterkurve oder einer raumfüllenden Kurve. Zunächst können Sie einen minimalen Spannbaum des Graphen berechnen und dann die längsten und teuersten Kanten entfernen. Dann macht der Baum viele kleine Bäume und Sie können die k-Means verwenden, um eine Gruppe von Punkten zu berechnen, dh Cluster.
"Der Single-Link-k-Clustering-Algorithmus ... ist genau Kruskals Algorithmus ... gleichbedeutend mit dem Finden eines MST und dem Löschen der k-1 teuersten Kanten." Siehe zum Beispiel hier:https://stats.stackexchange.com/ questions/1475/visualization-software-for-clustering .
Ein gutes Beispiel für eine Monsterkurve ist die Hilbert-Kurve. Die Grundform dieser Kurve ist eine U-Form und indem viele davon zusammenkopiert und gedreht werden, füllt die Kurve den euklidischen Raum aus. Überraschenderweise kann ein Gray-Code helfen, die Orientierung dieser U-Form herauszufinden. Sie können Nicks räumlichen Index Quadtree Hilbert Curve nachschlagen Blogartikel über mehr Details . Anstatt den Index der Kurve zu berechnen, können Sie einen Quadkey wie in Bing Maps zusammenstellen. Der Quadkey ist für jede Koordinate eindeutig und kann mit normalen Zeichenfolgenoperationen verwendet werden. Jede Position in der Taste ist Teil der U-förmigen Kurve und somit können Sie diesen Punktbereich teilweise von links nach rechts aus der Quadtaste auswählen.
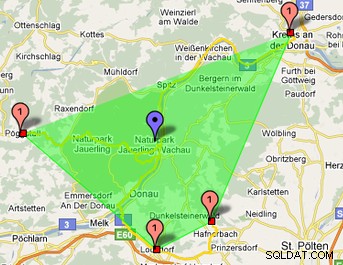
In diesem Bild sehen Sie, dass das grüne Polygon mithilfe einer Hilbert-Kurve gefunden wird:
Sie finden meine PHP-Klassen hier:https://www.phpclasses.org/package/6202-PHP-Generate-points-of-an-Hilbert-curve.html