Database
 sql >> Datenbank >  >> RDS >> Database

Angebot an Nachfrage anpassen – Lösungen, Teil 2

[ Springe zu:Ursprüngliche Herausforderung | Lösungen:Teil 1 | Teil 2 | Teil 3 ]

In diesem Artikel setze ich die Berichterstattung über Lösungen für Peter Larssons verlockende Matching-Herausforderung von Angebot und Nachfrage fort. Nochmals vielen Dank an Luca, Kamil Kosno, Daniel Brown, Brian Walker, Joe Obbish, Rainer Hoffmann, Paul White, Charlie und Peter Larsson für die Zusendung Ihrer Lösungen.

Letzten Monat habe ich eine Lösung behandelt, die auf Intervallschnittpunkten basiert, wobei ich einen klassischen prädikatbasierten Intervallschnitttest verwendet habe. Ich werde diese Lösung als klassische Kreuzungen bezeichnen . Der klassische Intervallschnittansatz führt zu einem Plan mit quadratischer Skalierung (N^2). Ich habe seine schlechte Leistung anhand von Beispieleingaben im Bereich von 100.000 bis 400.000 Zeilen demonstriert. Es dauerte 931 Sekunden, bis die Lösung gegen die 400.000-Zeilen-Eingabe abgeschlossen war! Diesen Monat beginne ich damit, Sie kurz an die Lösung vom letzten Monat zu erinnern und warum sie so schlecht skaliert und funktioniert. Anschließend stelle ich einen Ansatz vor, der auf einer Überarbeitung des Intervallschnitttests basiert. Dieser Ansatz wurde von Luca, Kamil und möglicherweise auch Daniel verwendet und ermöglicht eine Lösung mit viel besserer Leistung und Skalierung. Ich werde diese Lösung als überarbeitete Schnittpunkte bezeichnen .

Das Problem mit dem klassischen Schnittpunkttest

Beginnen wir mit einer kurzen Erinnerung an die Lösung vom letzten Monat.

Ich habe die folgenden Indizes in der Eingabetabelle dbo.Auctions verwendet, um die Berechnung der laufenden Summen zu unterstützen, die die Nachfrage- und Angebotsintervalle erzeugen:

-- Index to support solution
 
CREATE UNIQUE NONCLUSTERED INDEX idx_Code_ID_i_Quantity
  ON dbo.Auctions(Code, ID)
  INCLUDE(Quantity);
 
-- Enable batch-mode Window Aggregate
 
CREATE NONCLUSTERED COLUMNSTORE INDEX idx_cs
  ON dbo.Auctions(ID)
  WHERE ID = -1 AND ID = -2;

Der folgende Code enthält die vollständige Lösung, die den klassischen Intervallschnittansatz implementiert:

-- Drop temp tables if exist
 
SET NOCOUNT ON;
DROP TABLE IF EXISTS #MyPairings, #Demand, #Supply;
GO
 
WITH D0 AS
 
-- D0 computes running demand as EndDemand
 
(
  SELECT ID, Quantity,
    SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand
  FROM dbo.Auctions
  WHERE Code = 'D'
),
 
-- D extracts prev EndDemand as StartDemand, expressing start-end demand as an interval
 
D AS
(
  SELECT ID, Quantity, EndDemand - Quantity AS StartDemand, EndDemand
  FROM D0
)
SELECT ID,
  CAST(ISNULL(StartDemand, 0.0) AS DECIMAL(19, 6)) AS StartDemand,
  CAST(ISNULL(EndDemand,   0.0) AS DECIMAL(19, 6)) AS EndDemand
INTO #Demand
FROM D;
 
WITH S0 AS
 
-- S0 computes running supply as EndSupply
 
(
  SELECT ID, Quantity,
    SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndSupply
  FROM dbo.Auctions
  WHERE Code = 'S'
),
 
-- S extracts prev EndSupply as StartSupply, expressing start-end supply as an interval
 
S AS
(
  SELECT ID, Quantity, EndSupply - Quantity AS StartSupply, EndSupply
  FROM S0
)
SELECT ID, 
  CAST(ISNULL(StartSupply, 0.0) AS DECIMAL(19, 6)) AS StartSupply,
  CAST(ISNULL(EndSupply, 0.0) AS DECIMAL(19, 6)) AS EndSupply
INTO #Supply
FROM S;
 
CREATE UNIQUE CLUSTERED INDEX idx_cl_ES_ID ON #Supply(EndSupply, ID);
 
-- Trades are the overlapping segments of the intersecting intervals
 
SELECT
  D.ID AS DemandID, S.ID AS SupplyID,
  CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
    AS TradeQuantity
INTO #MyPairings
FROM #Demand AS D
  INNER JOIN #Supply AS S WITH (FORCESEEK)
    ON D.StartDemand < S.EndSupply AND D.EndDemand > S.StartSupply;

Dieser Code beginnt mit der Berechnung der Bedarfs- und Angebotsintervalle und schreibt diese in temporäre Tabellen mit den Namen #Demand und #Supply. Der Code erstellt dann einen gruppierten Index auf #Supply mit EndSupply als führendem Schlüssel, um den Schnittmengentest bestmöglich zu unterstützen. Schließlich verbindet der Code #Supply und #Demand und identifiziert Trades als die überlappenden Segmente der sich überschneidenden Intervalle, wobei das folgende Join-Prädikat basierend auf dem klassischen Intervall-Schnittpunkttest verwendet wird:

D.StartDemand < S.EndSupply AND D.EndDemand > S.StartSupply

Der Plan für diese Lösung ist in Abbildung 1 dargestellt.

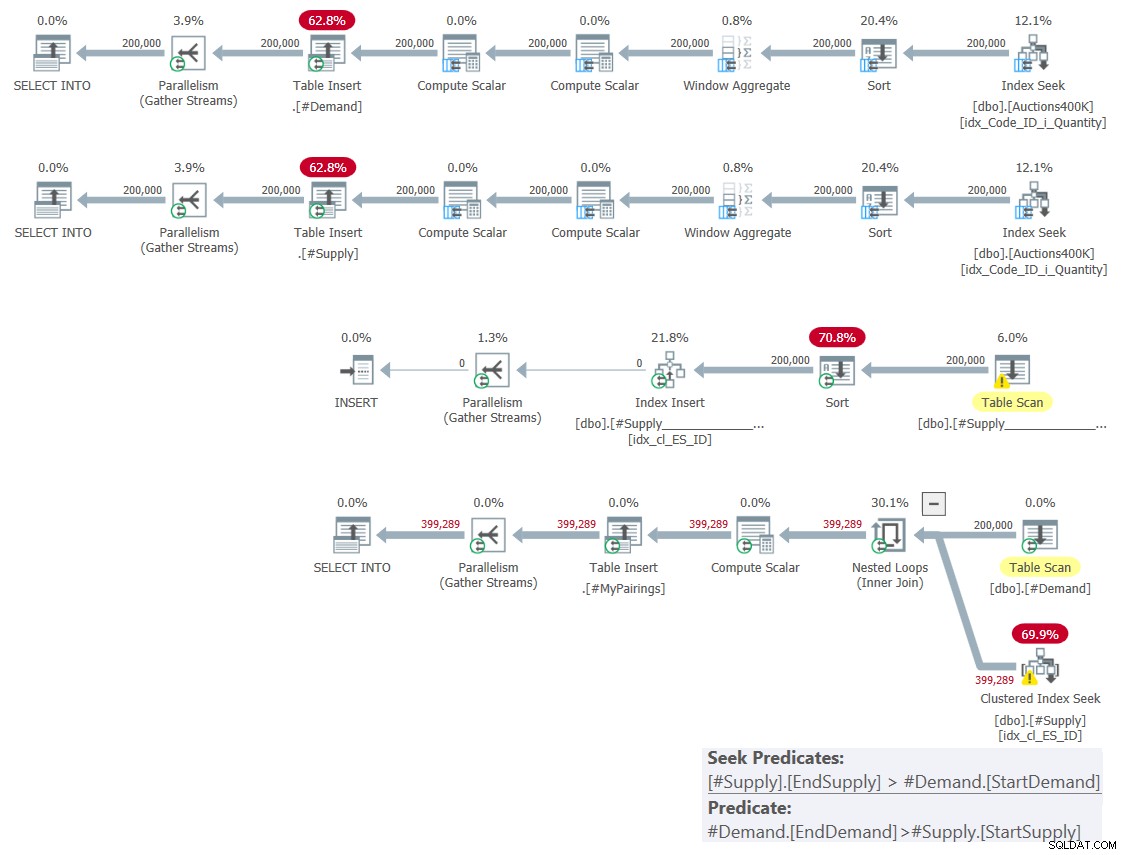Abbildung 1:Abfrageplan für Lösung basierend auf klassischen Schnittpunkten

Wie ich letzten Monat erklärt habe, kann nur eines der beiden beteiligten Bereichsprädikate als Suchprädikat im Rahmen einer Indexsuchoperation verwendet werden, während das andere als Restprädikat angewendet werden muss. Sie können dies deutlich im Plan für die letzte Abfrage in Abbildung 1 sehen. Deshalb habe ich mir die Mühe gemacht, nur einen Index auf einer der Tabellen zu erstellen. Ich habe auch die Verwendung einer Suche in dem Index erzwungen, den ich mit dem FORCESEEK-Hinweis erstellt habe. Anderenfalls könnte der Optimierer diesen Index ignorieren und mithilfe eines Index-Spool-Operators einen eigenen erstellen.

Dieser Plan hat quadratische Komplexität, da pro Zeile auf der einen Seite – in unserem Fall #Demand – die Indexsuche auf der anderen Seite – in unserem Fall #Supply – basierend auf dem Suchprädikat durchschnittlich auf die Hälfte der Zeilen zugreifen und die identifizieren muss endgültige Übereinstimmungen durch Anwendung des Restprädikats.

Wenn Ihnen immer noch unklar ist, warum dieser Plan eine quadratische Komplexität hat, könnte vielleicht eine visuelle Darstellung der Arbeit helfen, wie in Abbildung 2 gezeigt.

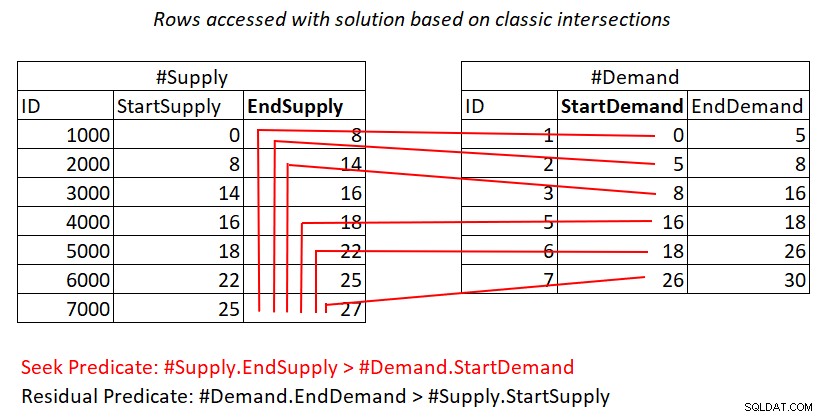Abbildung 2:Darstellung der Arbeit mit Lösung basierend auf klassischen Schnittpunkten

Diese Abbildung stellt die Arbeit dar, die der Nested Loops-Join im Plan für die letzte Abfrage geleistet hat. Der #Demand-Heap ist die äußere Eingabe des Joins und der gruppierte Index auf #Supply (mit EndSupply als führendem Schlüssel) ist die innere Eingabe. Die roten Linien stellen die Indexsuchaktivitäten dar, die pro Zeile in #Demand im Index auf #Supply ausgeführt werden, und die Zeilen, auf die sie als Teil der Range-Scans im Indexblatt zugreifen. Bei extrem niedrigen StartDemand-Werten in #Demand muss der Bereichsscan auf nahezu alle Zeilen in #Supply zugreifen. Bei extrem hohen StartDemand-Werten in #Demand muss der Bereichsscan auf nahezu null Zeilen in #Supply zugreifen. Im Durchschnitt muss der Bereichsscan auf etwa die Hälfte der Zeilen in #Supply pro nachgefragter Zeile zugreifen. Bei D Nachfragezeilen und S Angebotszeilen ist die Anzahl der Zeilen, auf die zugegriffen wird, D + D*S/2. Das kommt zu den Kosten für die Suchen hinzu, die Sie zu den passenden Zeilen bringen. Wenn Sie beispielsweise dbo.Auctions mit 200.000 Nachfragezeilen und 200.000 Angebotszeilen füllen, bedeutet dies, dass der Nested Loops-Join auf 200.000 Nachfragezeilen + 200.000*200.000/2 Angebotszeilen zugreift, oder 200.000 + 200.000^2/2 =20.000.200.000 Zeilen, auf die zugegriffen wird. Hier werden viele Versorgungsreihen neu gescannt!

Wenn Sie an der Idee der Intervallschnittpunkte festhalten, aber eine gute Leistung erzielen möchten, müssen Sie einen Weg finden, den Arbeitsaufwand zu reduzieren.

In seiner Lösung hat Joe Obbish die Intervalle basierend auf der maximalen Intervalllänge gebuckelt. Auf diese Weise konnte er die Anzahl der Zeilen reduzieren, die die Joins verarbeiten mussten, und sich auf die Stapelverarbeitung verlassen. Als abschließenden Filter verwendete er den klassischen Intervallschnitttest. Joes Lösung funktioniert gut, solange die maximale Intervalllänge nicht sehr hoch ist, aber die Laufzeit der Lösung steigt mit zunehmender maximaler Intervalllänge.

Also, was können Sie sonst noch tun …?

Überarbeiteter Schnittpunkttest

Luca, Kamil und möglicherweise Daniel (es gab einen unklaren Teil seiner geposteten Lösung aufgrund der Formatierung der Website, also musste ich raten) verwendeten einen überarbeiteten Intervallschnitttest, der eine viel bessere Nutzung der Indizierung ermöglicht.

Ihr Schnittpunkttest ist eine Disjunktion zweier Prädikate (Prädikate getrennt durch einen ODER-Operator):

   (D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply) OR (S.StartSupply >= D.StartDemand AND S.StartSupply < D.EndDemand)

Im Englischen schneidet sich entweder der Bedarfsstartbegrenzer mit dem Versorgungsintervall in einer inklusiven, exklusiven Weise (einschließlich des Starts und ohne das Ende); oder das Angebotsstart-Begrenzungszeichen schneidet das Bedarfsintervall in einer inklusiven, exklusiven Weise. Um die beiden Prädikate disjunkt zu machen (keine überlappenden Fälle zu haben), aber dennoch alle Fälle abzudecken, können Sie den =-Operator nur in dem einen oder anderen beibehalten, zum Beispiel:

   (D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply) OR (S.StartSupply > D.StartDemand AND S.StartSupply < D.EndDemand)

Dieser überarbeitete Intervallschnitttest ist sehr aufschlussreich. Jedes der Prädikate kann potenziell effizient einen Index verwenden. Betrachten Sie Prädikat 1:

D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply
^^^^^^^^^^^^^                      ^^^^^^^^^^^^^

Angenommen, Sie erstellen einen abdeckenden Index auf #Demand mit StartDemand als führendem Schlüssel, können Sie möglicherweise einen Nested-Loops-Join erhalten, indem Sie die in Abbildung 3 dargestellte Arbeit anwenden.


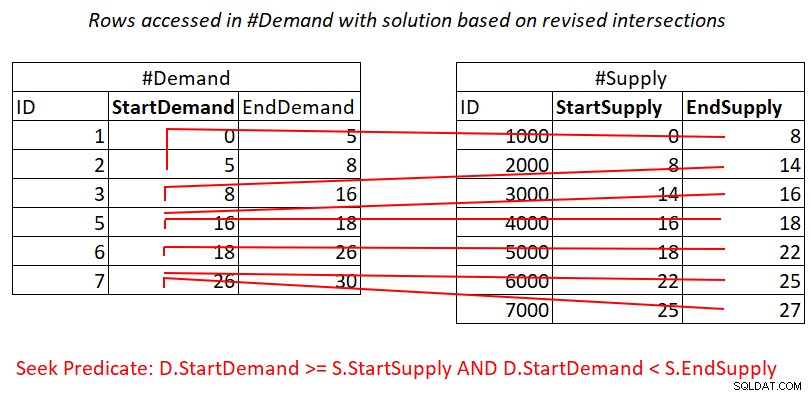
Abbildung 3:Veranschaulichung der theoretischen Arbeit, die zum Verarbeiten von Prädikat erforderlich ist 1

Ja, Sie zahlen immer noch für eine Suche im #Demand-Index pro Zeile in #Supply, aber die Bereichsscans im Indexblatt greifen auf fast unzusammenhängende Teilmengen von Zeilen zu. Kein erneutes Scannen von Zeilen!

Ähnlich verhält es sich mit Prädikat 2:

S.StartSupply > D.StartDemand AND S.StartSupply < D.EndDemand
^^^^^^^^^^^^^                     ^^^^^^^^^^^^^

Angenommen, Sie erstellen einen abdeckenden Index für #Supply mit StartSupply als führendem Schlüssel, können Sie möglicherweise einen Nested-Loops-Join erhalten, indem Sie die in Abbildung 4 dargestellte Arbeit anwenden.


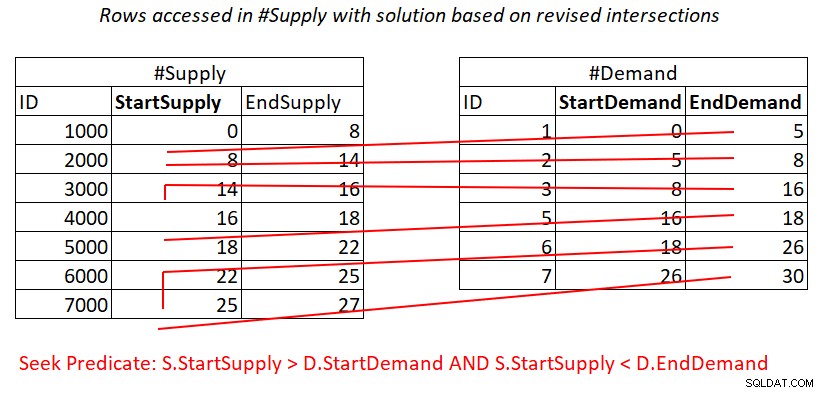
Abbildung 4:Veranschaulichung der theoretischen Arbeit, die zum Verarbeiten von Prädikat erforderlich ist 2

Außerdem zahlen Sie hier für eine Suche im #Supply-Index pro Zeile in #Demand, und dann greifen die Bereichsscans im Indexblatt auf fast unzusammenhängende Teilmengen von Zeilen zu. Auch hier kein erneutes Scannen von Zeilen!

Unter der Annahme von D Nachfragezeilen und S Angebotszeilen kann die Arbeit wie folgt beschrieben werden:

Number of index seek operations: D  + S
Number of rows accessed:         2D + 2S

Der größte Teil der Kosten sind also wahrscheinlich die I/O-Kosten, die mit den Suchvorgängen verbunden sind. Aber dieser Teil der Arbeit hat eine lineare Skalierung im Vergleich zur quadratischen Skalierung der klassischen Intervallschnittpunktabfrage.

Natürlich müssen Sie die vorläufigen Kosten für die Indexerstellung auf den temporären Tabellen berücksichtigen, die aufgrund der damit verbundenen Sortierung eine n log n-Skalierung aufweisen, aber Sie zahlen diesen Teil als vorläufigen Teil beider Lösungen.

Lassen Sie uns versuchen, diese Theorie in die Praxis umzusetzen. Beginnen wir damit, die temporären Tabellen #Demand und #supply mit den Nachfrage- und Angebotsintervallen zu füllen (wie bei den klassischen Intervallschnittpunkten) und die unterstützenden Indizes zu erstellen:

-- Drop temp tables if exist
 
SET NOCOUNT ON;
DROP TABLE IF EXISTS #MyPairings, #Demand, #Supply;
GO
 
WITH D0 AS
 
-- D0 computes running demand as EndDemand
 
(
  SELECT ID, Quantity,
    SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand
  FROM dbo.Auctions
  WHERE Code = 'D'
),
 
-- D extracts prev EndDemand as StartDemand, expressing start-end demand as an interval
 
D AS
(
  SELECT ID, Quantity, EndDemand - Quantity AS StartDemand, EndDemand
  FROM D0
)
SELECT ID, 
  CAST(ISNULL(StartDemand, 0.0) AS DECIMAL(19, 6)) AS StartDemand,
  CAST(ISNULL(EndDemand,   0.0) AS DECIMAL(19, 6)) AS EndDemand
INTO #Demand
FROM D;
 
WITH S0 AS
 
-- S0 computes running supply as EndSupply
 
(
  SELECT ID, Quantity,
    SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndSupply
  FROM dbo.Auctions
  WHERE Code = 'S'
),
 
-- S extracts prev EndSupply as StartSupply, expressing start-end supply as an interval
 
S AS
(
  SELECT ID, Quantity, EndSupply - Quantity AS StartSupply, EndSupply
  FROM S0
)
SELECT ID, 
  CAST(ISNULL(StartSupply, 0.0) AS DECIMAL(19, 6)) AS StartSupply,
  CAST(ISNULL(EndSupply,   0.0) AS DECIMAL(19, 6)) AS EndSupply
INTO #Supply
FROM S;
 
-- Indexing
 
CREATE UNIQUE CLUSTERED INDEX idx_cl_SD_ID ON #Demand(StartDemand, ID);
CREATE UNIQUE CLUSTERED INDEX idx_cl_SS_ID ON #Supply(StartSupply, ID);

Die Pläne zum Füllen der temporären Tabellen und zum Erstellen der Indizes sind in Abbildung 5 dargestellt.


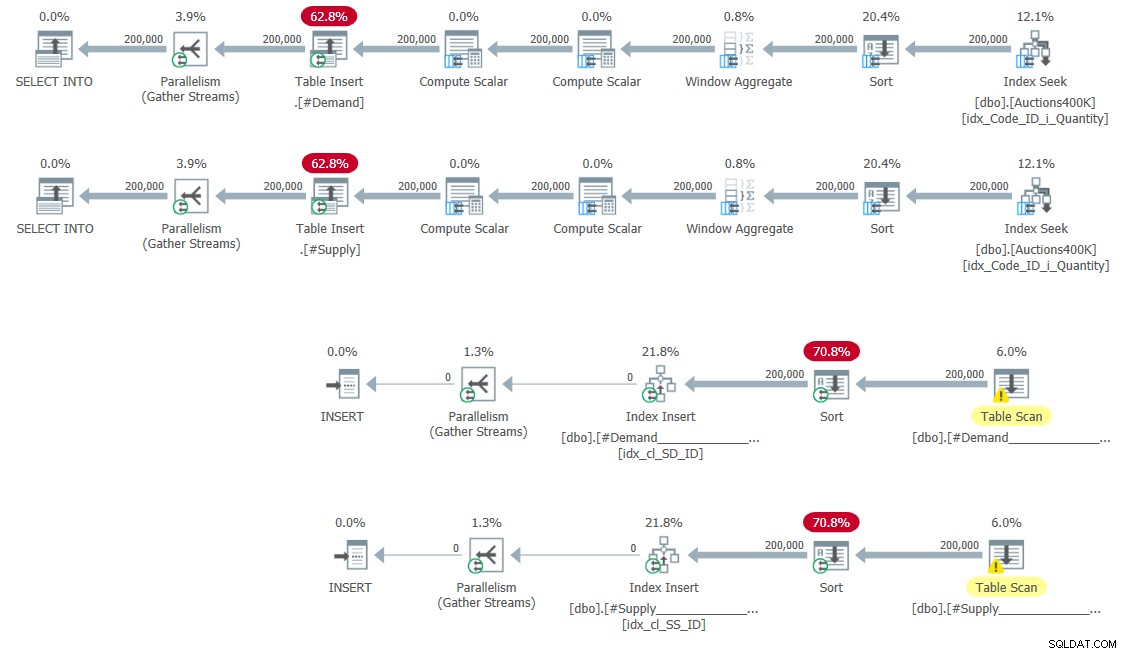
Abbildung 5:Abfragepläne zum Füllen temporärer Tabellen und zum Erstellen Indizes

Hier gibt es keine Überraschungen.

Nun zur letzten Abfrage. Sie könnten versucht sein, eine einzige Abfrage mit der oben erwähnten Disjunktion zweier Prädikate zu verwenden, etwa so:

SELECT
  D.ID AS DemandID, S.ID AS SupplyID,
  CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
    AS TradeQuantity
INTO #MyPairings
FROM #Demand AS D
  INNER JOIN #Supply AS S
    ON (D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply) OR (S.StartSupply >  D.StartDemand AND S.StartSupply < D.EndDemand);

Der Plan für diese Abfrage ist in Abbildung 6 dargestellt.


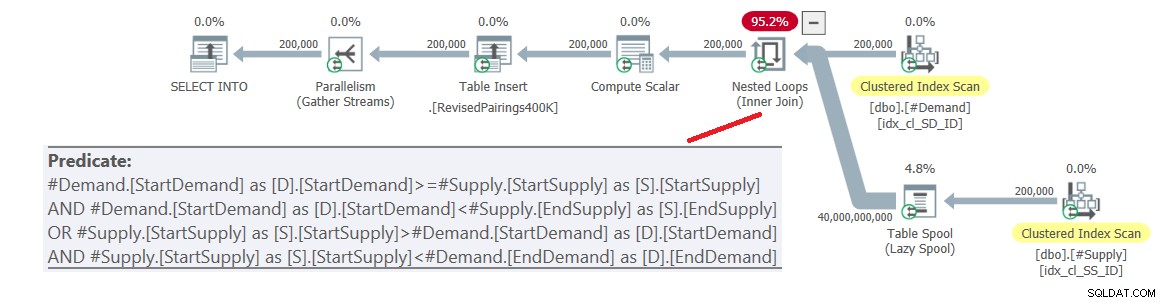
Abbildung 6:Abfrageplan für die endgültige Abfrage mit überarbeiteter Schnittmenge testen, versuchen 1

Das Problem besteht darin, dass der Optimierer nicht weiß, wie er diese Logik in zwei separate Aktivitäten aufteilen kann, die jeweils ein anderes Prädikat handhaben und den jeweiligen Index effizient nutzen. Es endet also mit einem vollständigen kartesischen Produkt der beiden Seiten, wobei alle Prädikate als Restprädikate angewendet werden. Mit 200.000 Nachfragezeilen und 200.000 Angebotszeilen verarbeitet der Join 40.000.000.000 Zeilen.

Der aufschlussreiche Trick von Luca, Kamil und möglicherweise Daniel bestand darin, die Logik in zwei Abfragen aufzuteilen und ihre Ergebnisse zu vereinheitlichen. Hier wird es wichtig, zwei disjunkte Prädikate zu verwenden! Sie können anstelle von UNION einen UNION ALL-Operator verwenden, um unnötige Kosten für die Suche nach Duplikaten zu vermeiden. Hier ist die Abfrage, die diesen Ansatz implementiert:

SELECT
  D.ID AS DemandID, S.ID AS SupplyID,
  CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
    AS TradeQuantity
INTO #MyPairings
FROM #Demand AS D
  INNER JOIN #Supply AS S
    ON D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply
 
UNION ALL
 
SELECT
  D.ID AS DemandID, S.ID AS SupplyID,
  CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
    AS TradeQuantity
FROM #Demand AS D
  INNER JOIN #Supply AS S
    ON S.StartSupply > D.StartDemand AND S.StartSupply < D.EndDemand;

Der Plan für diese Abfrage ist in Abbildung 7 dargestellt.


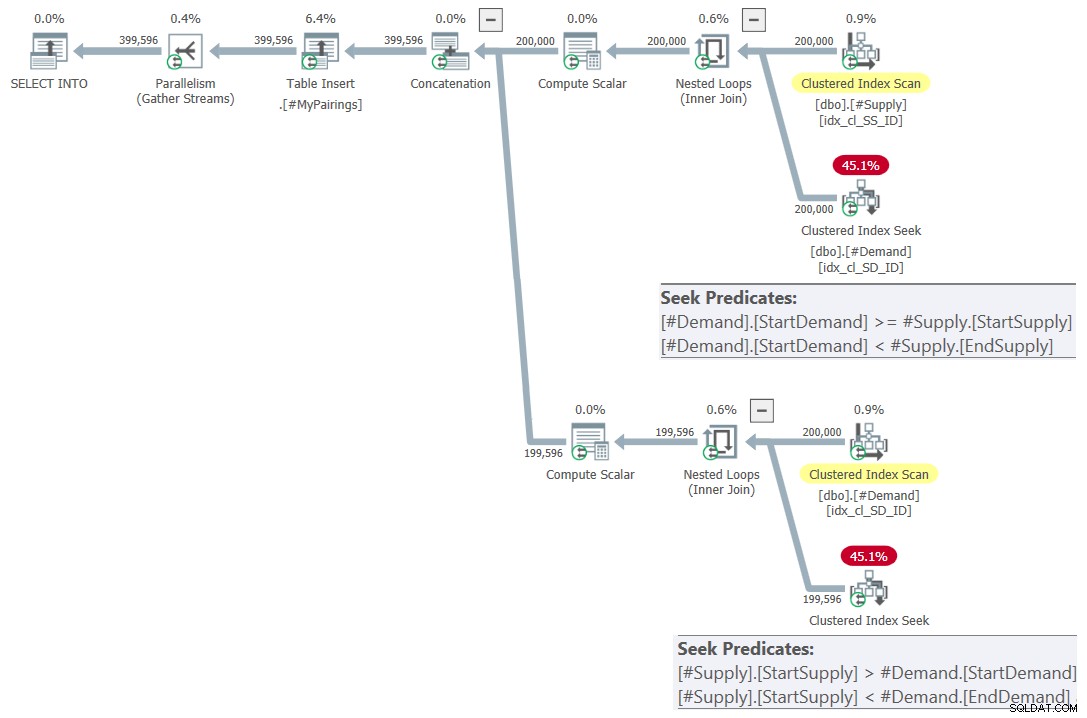
Abbildung 7:Abfrageplan für die endgültige Abfrage mit überarbeiteter Schnittmenge testen, versuchen 2

Das ist einfach schön! Ist es nicht? Und weil es so schön ist, hier ist die gesamte Lösung von Grund auf neu, einschließlich der Erstellung temporärer Tabellen, der Indizierung und der abschließenden Abfrage:

-- Drop temp tables if exist
 
SET NOCOUNT ON;
DROP TABLE IF EXISTS #MyPairings, #Demand, #Supply;
GO
 
WITH D0 AS
 
-- D0 computes running demand as EndDemand
 
(
  SELECT ID, Quantity,
    SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand
  FROM dbo.Auctions
  WHERE Code = 'D'
),
 
-- D extracts prev EndDemand as StartDemand, expressing start-end demand as an interval
 
D AS
(
  SELECT ID, Quantity, EndDemand - Quantity AS StartDemand, EndDemand
  FROM D0
)
SELECT ID, 
  CAST(ISNULL(StartDemand, 0.0) AS DECIMAL(19, 6)) AS StartDemand,
  CAST(ISNULL(EndDemand,   0.0) AS DECIMAL(19, 6)) AS EndDemand
INTO #Demand
FROM D;
 
WITH S0 AS
 
-- S0 computes running supply as EndSupply
 
(
  SELECT ID, Quantity,
    SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndSupply
  FROM dbo.Auctions
  WHERE Code = 'S'
),
 
-- S extracts prev EndSupply as StartSupply, expressing start-end supply as an interval
 
S AS
(
  SELECT ID, Quantity, EndSupply - Quantity AS StartSupply, EndSupply
  FROM S0
)
SELECT ID,
  CAST(ISNULL(StartSupply, 0.0) AS DECIMAL(19, 6)) AS StartSupply,
  CAST(ISNULL(EndSupply,   0.0) AS DECIMAL(19, 6)) AS EndSupply
INTO #Supply
FROM S;
 
-- Indexing
 
CREATE UNIQUE CLUSTERED INDEX idx_cl_SD_ID ON #Demand(StartDemand, ID);
CREATE UNIQUE CLUSTERED INDEX idx_cl_SS_ID ON #Supply(StartSupply, ID);
 
-- Trades are the overlapping segments of the intersecting intervals
 
SELECT
  D.ID AS DemandID, S.ID AS SupplyID,
  CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
    AS TradeQuantity
INTO #MyPairings
FROM #Demand AS D
  INNER JOIN #Supply AS S
    ON D.StartDemand >= S.StartSupply AND D.StartDemand < S.EndSupply
 
UNION ALL
 
SELECT
  D.ID AS DemandID, S.ID AS SupplyID,
  CASE WHEN EndDemand < EndSupply THEN EndDemand ELSE EndSupply END - CASE WHEN StartDemand > StartSupply THEN StartDemand ELSE StartSupply END
    AS TradeQuantity
FROM #Demand AS D
  INNER JOIN #Supply AS S
    ON S.StartSupply > D.StartDemand AND S.StartSupply < D.EndDemand;

Wie bereits erwähnt, bezeichne ich diese Lösung als überarbeitete Schnittpunkte .

Kamils ​​Lösung

Unter den Lösungen von Luca, Kamil und Daniel war die von Kamil die schnellste. Hier ist Kamils ​​vollständige Lösung:

SET NOCOUNT ON;
DROP TABLE IF EXISTS #supply, #demand;
GO
 
CREATE TABLE #demand
(
  DemandID           INT NOT NULL,
  DemandQuantity     DECIMAL(19, 6) NOT NULL,
  QuantityFromDemand DECIMAL(19, 6) NOT NULL,
  QuantityToDemand   DECIMAL(19, 6) NOT NULL
);
 
CREATE TABLE #supply
(
  SupplyID           INT NOT NULL,
  QuantityFromSupply DECIMAL(19, 6) NOT NULL,
  QuantityToSupply   DECIMAL(19,6) NOT NULL
);
 
WITH demand AS
(
  SELECT
    a.ID AS DemandID,
    a.Quantity AS DemandQuantity,
    SUM(a.Quantity) OVER(ORDER BY ID ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW) 
      - a.Quantity AS QuantityFromDemand,
    SUM(a.Quantity) OVER(ORDER BY ID ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW) 
      AS QuantityToDemand
  FROM dbo.Auctions AS a WHERE Code = 'D'
)
INSERT INTO #demand
(
  DemandID,
  DemandQuantity,
  QuantityFromDemand,
  QuantityToDemand
)
SELECT
  d.DemandID,
  d.DemandQuantity,
  d.QuantityFromDemand,
  d.QuantityToDemand
FROM demand AS d;
 
WITH supply AS
(
  SELECT
    a.ID AS SupplyID,
    SUM(a.Quantity) OVER(ORDER BY ID ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW) 
      - a.Quantity AS QuantityFromSupply,
    SUM(a.Quantity) OVER(ORDER BY ID ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW) 
      AS QuantityToSupply
  FROM dbo.Auctions AS a WHERE Code = 'S'
)
INSERT INTO #supply
(
  SupplyID,
  QuantityFromSupply,
  QuantityToSupply
)
SELECT
  s.SupplyID,
  s.QuantityFromSupply,
  s.QuantityToSupply
FROM supply AS s;
 
CREATE UNIQUE INDEX ix_1 ON #demand(QuantityFromDemand) 
  INCLUDE(DemandID, DemandQuantity, QuantityToDemand);
CREATE UNIQUE INDEX ix_1 ON #supply(QuantityFromSupply) 
  INCLUDE(SupplyID, QuantityToSupply);
CREATE NONCLUSTERED COLUMNSTORE INDEX nci ON #demand(DemandID) 
  WHERE DemandID is null;
 
DROP TABLE IF EXISTS #myPairings;
 
CREATE TABLE #myPairings
(
  DemandID      INT NOT NULL,
  SupplyID      INT NOT NULL,
  TradeQuantity DECIMAL(19, 6) NOT NULL
);
 
INSERT INTO #myPairings(DemandID, SupplyID, TradeQuantity) 
  SELECT
    d.DemandID,
    s.SupplyID, 
    d.DemandQuantity
      - CASE WHEN d.QuantityFromDemand < s.QuantityFromSupply 
             THEN s.QuantityFromSupply - d.QuantityFromDemand ELSE 0 end
      - CASE WHEN s.QuantityToSupply < d.QuantityToDemand 
             THEN d.QuantityToDemand - s.QuantityToSupply ELSE 0 END AS TradeQuantity 
  FROM #demand AS d 
    INNER JOIN #supply AS s 
      ON (d.QuantityFromDemand < s.QuantityToSupply 
          AND s.QuantityFromSupply <= d.QuantityFromDemand)
 
  UNION ALL
 
  SELECT
    d.DemandID,
    s.SupplyID,
    d.DemandQuantity
      - CASE WHEN d.QuantityFromDemand < s.QuantityFromSupply 
             THEN s.QuantityFromSupply - d.QuantityFromDemand ELSE 0 END
      - CASE WHEN s.QuantityToSupply < d.QuantityToDemand 
             THEN d.QuantityToDemand - s.QuantityToSupply ELSE 0 END AS TradeQuantity
  FROM #supply AS s 
    INNER JOIN #demand AS d 
      ON (s.QuantityFromSupply < d.QuantityToDemand 
          AND d.QuantityFromDemand < s.QuantityFromSupply);

Wie Sie sehen können, kommt es der überarbeiteten Kreuzungslösung, die ich behandelt habe, sehr nahe.

Der Plan für die letzte Abfrage in Kamils ​​Lösung ist in Abbildung 8 dargestellt.


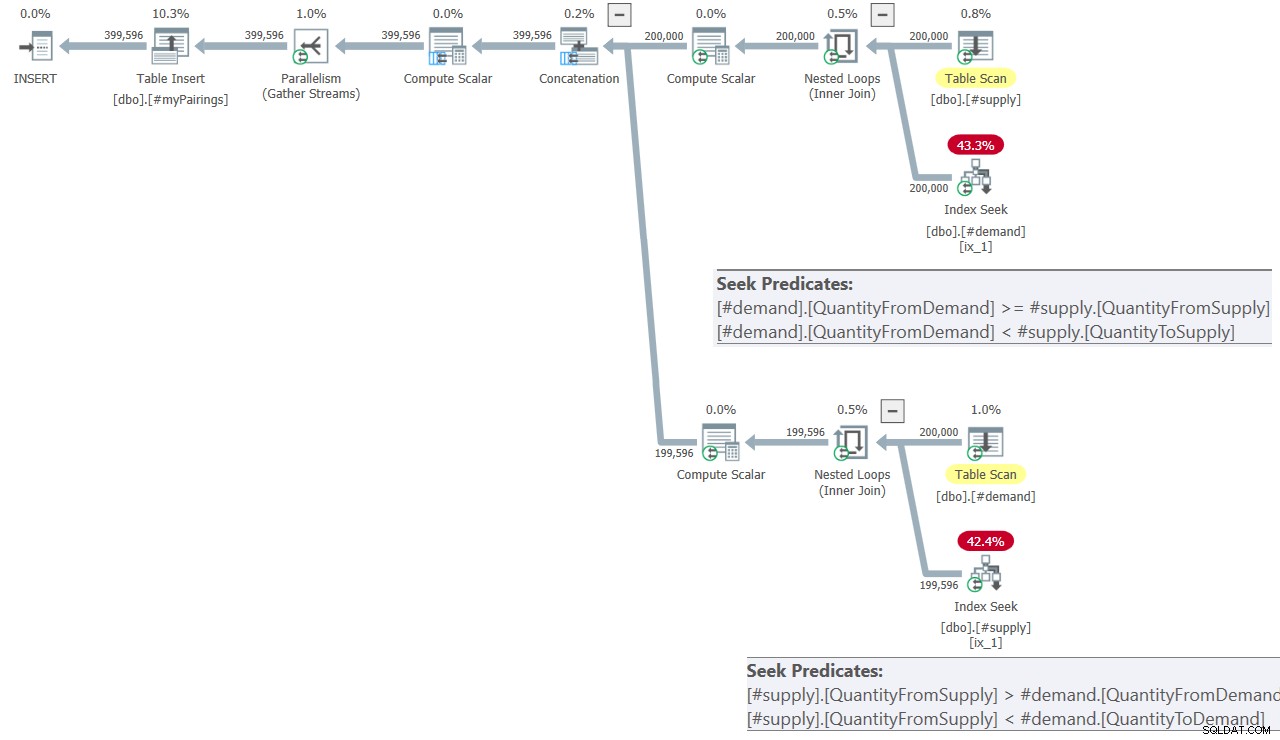
Abbildung 8:Abfrageplan für die letzte Abfrage in Kamils ​​Lösung

Der Plan sieht dem zuvor in Abbildung 7 gezeigten ziemlich ähnlich.

Leistungstest

Erinnern Sie sich daran, dass die klassische Schnittpunktlösung 931 Sekunden benötigte, um sie gegen eine Eingabe mit 400.000 Zeilen abzuschließen. Das sind 15 Minuten! Es ist viel, viel schlimmer als die Cursor-Lösung, die ungefähr 12 Sekunden dauerte, um mit derselben Eingabe fertig zu werden. Abbildung 9 enthält die Leistungszahlen einschließlich der in diesem Artikel besprochenen neuen Lösungen.


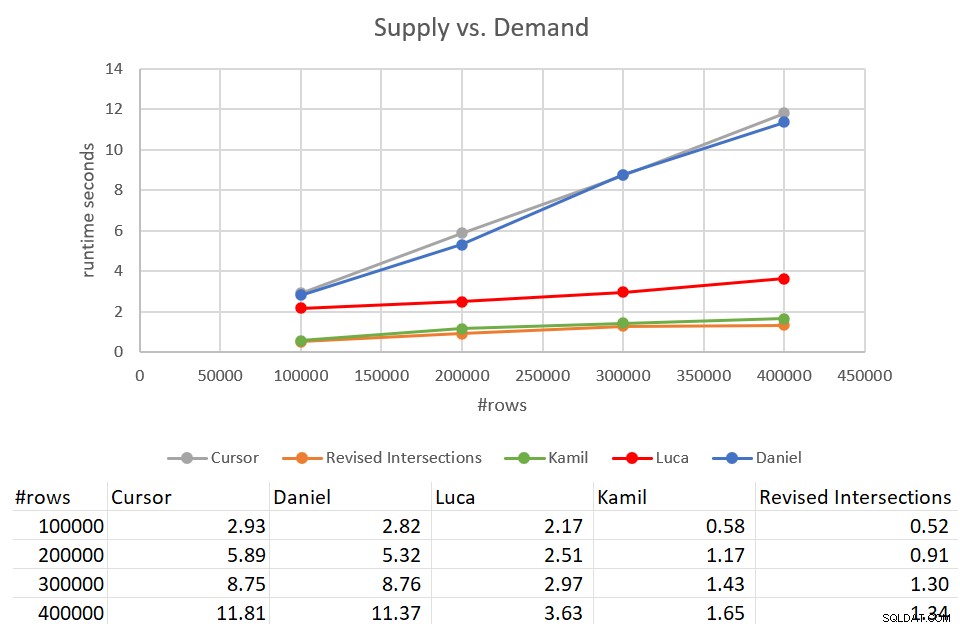
Abbildung 9:Leistungstest

Wie Sie sehen können, dauerten die Lösung von Kamil und die ähnlich überarbeitete Lösung für Schnittpunkte etwa 1,5 Sekunden, um mit der 400.000-Zeilen-Eingabe fertig zu werden. Das ist eine ziemlich anständige Verbesserung im Vergleich zur ursprünglichen Cursor-basierten Lösung. Der Hauptnachteil dieser Lösungen sind die I/O-Kosten. Mit einer Suche pro Zeile führen diese Lösungen bei einer Eingabe von 400.000 Zeilen mehr als 1,35 Millionen Lesevorgänge durch. Angesichts der guten Laufzeit und Skalierung, die Sie erhalten, könnte dies jedoch auch als absolut akzeptabler Preis angesehen werden.

Was kommt als Nächstes?

Unser erster Versuch, die Matching-Herausforderung von Angebot und Nachfrage zu lösen, stützte sich auf den klassischen Interval-Schnittpunkttest und erhielt einen schlecht funktionierenden Plan mit quadratischer Skalierung. Viel schlimmer als die Cursor-basierte Lösung. Basierend auf den Erkenntnissen von Luca, Kamil und Daniel war unser zweiter Versuch unter Verwendung eines überarbeiteten Intervallschnitttests eine signifikante Verbesserung, die die Indizierung effizient nutzt und eine bessere Leistung als die Cursor-basierte Lösung erbringt. Diese Lösung ist jedoch mit erheblichen I/O-Kosten verbunden. Nächsten Monat werde ich weiter nach weiteren Lösungen suchen.

[ Springe zu:Ursprüngliche Herausforderung | Lösungen:Teil 1 | Teil 2 | Teil 3 ]