SQL Server hat sich traditionell davor gescheut, native Lösungen für einige der häufigeren statistischen Fragen bereitzustellen, wie z. B. die Berechnung eines Medians. Laut WikiPedia wird „Median als der numerische Wert beschrieben, der die obere Hälfte einer Stichprobe, einer Grundgesamtheit oder einer Wahrscheinlichkeitsverteilung von der unteren Hälfte trennt. Der Median einer endlichen Liste von Zahlen kann gefunden werden, indem man alle Beobachtungen anordnet niedrigsten Wert zum höchsten Wert und Auswahl des mittleren. Wenn es eine gerade Anzahl von Beobachtungen gibt, dann gibt es keinen einzigen mittleren Wert; der Median wird dann normalerweise als Mittelwert der beiden mittleren Werte definiert."
In Bezug auf eine SQL Server-Abfrage ist das Wichtigste, was Sie daraus mitnehmen, dass Sie alle Werte "anordnen" (sortieren) müssen. Das Sortieren in SQL Server ist normalerweise eine ziemlich teure Operation, wenn es keinen unterstützenden Index gibt, und das Hinzufügen eines Index zur Unterstützung einer Operation, die wahrscheinlich nicht so oft angefordert wird, lohnt sich möglicherweise nicht.
Lassen Sie uns untersuchen, wie wir dieses Problem in früheren Versionen von SQL Server normalerweise gelöst haben. Lassen Sie uns zuerst eine sehr einfache Tabelle erstellen, damit wir prüfen können, ob unsere Logik korrekt ist, und einen genauen Median ableiten. Wir können die folgenden zwei Tabellen testen, eine mit einer geraden Zeilenzahl und die andere mit einer ungeraden Zeilenzahl:
CREATE TABLE dbo.EvenRows ( id INT PRIMARY KEY, val INT );
CREATE TABLE dbo.OddRows ( id INT PRIMARY KEY, val INT );
INSERT dbo.EvenRows(id,val)
SELECT 1, 6
UNION ALL SELECT 2, 11
UNION ALL SELECT 3, 4
UNION ALL SELECT 4, 4
UNION ALL SELECT 5, 15
UNION ALL SELECT 6, 14
UNION ALL SELECT 7, 4
UNION ALL SELECT 8, 9;
INSERT dbo.OddRows(id,val)
SELECT 1, 6
UNION ALL SELECT 2, 11
UNION ALL SELECT 3, 4
UNION ALL SELECT 4, 4
UNION ALL SELECT 5, 15
UNION ALL SELECT 6, 14
UNION ALL SELECT 7, 4;
DECLARE @Median DECIMAL(12, 2); Nur durch beiläufige Beobachtung können wir sehen, dass der Median für die Tabelle mit ungeraden Zeilen 6 sein sollte und für die geraden Tabellen 7,5 ((6+9)/2). Sehen wir uns nun einige Lösungen an, die im Laufe der Jahre verwendet wurden:
SQL Server 2000
In SQL Server 2000 waren wir auf einen sehr eingeschränkten T-SQL-Dialekt beschränkt. Ich untersuche diese Vergleichsoptionen, da einige Leute immer noch SQL Server 2000 ausführen und andere möglicherweise ein Upgrade durchgeführt haben, aber da ihre Medianberechnungen "damals" geschrieben wurden, könnte der Code heute immer noch so aussehen.
2000_A – Max der einen Hälfte, Min der anderen
Dieser Ansatz nimmt den höchsten Wert von den ersten 50 Prozent, den niedrigsten Wert von den letzten 50 Prozent und dividiert sie dann durch zwei. Dies funktioniert für gerade oder ungerade Zeilen, da im geraden Fall die beiden Werte die beiden mittleren Zeilen sind und im ungeraden Fall die beiden Werte tatsächlich aus derselben Zeile stammen.
SELECT @Median = (
(SELECT MAX(val) FROM
(SELECT TOP 50 PERCENT val
FROM dbo.EvenRows ORDER BY val, id) AS t)
+ (SELECT MIN(val) FROM
(SELECT TOP 50 PERCENT val
FROM dbo.EvenRows ORDER BY val DESC, id DESC) AS b)
) / 2.0; 2000_B – #Temp-Tabelle
Dieses Beispiel erstellt zuerst eine #temp-Tabelle und bestimmt mithilfe der gleichen Art von Mathematik wie oben die beiden "mittleren" Zeilen mit Hilfe einer zusammenhängenden IDENTITY Spalte sortiert nach der Val-Spalte. (Die Reihenfolge der Zuweisung von IDENTITY auf Werte kann man sich nur wegen des MAXDOP verlassen Einstellung.)
CREATE TABLE #x
(
i INT IDENTITY(1,1),
val DECIMAL(12, 2)
);
CREATE CLUSTERED INDEX v ON #x(val);
INSERT #x(val)
SELECT val
FROM dbo.EvenRows
ORDER BY val OPTION (MAXDOP 1);
SELECT @Median = AVG(val)
FROM #x AS x
WHERE EXISTS
(
SELECT 1
FROM #x
WHERE x.i - (SELECT MAX(i) / 2.0 FROM #x) IN (0, 0.5, 1)
);
SQL Server 2005, 2008, 2008 R2
SQL Server 2005 hat einige interessante neue Fensterfunktionen eingeführt, wie z. B. ROW_NUMBER() , was dazu beitragen kann, statistische Probleme wie den Median etwas einfacher zu lösen als in SQL Server 2000. Diese Ansätze funktionieren alle in SQL Server 2005 und höher:
2005_A – Reihennummern duellieren
Dieses Beispiel verwendet ROW_NUMBER() um die Werte einmal in jede Richtung auf und ab zu gehen, findet dann die "mittlere" ein oder zwei Zeilen basierend auf dieser Berechnung. Dies ist dem ersten obigen Beispiel ziemlich ähnlich, mit einfacherer Syntax:
SELECT @Median = AVG(1.0 * val)
FROM
(
SELECT val,
ra = ROW_NUMBER() OVER (ORDER BY val, id),
rd = ROW_NUMBER() OVER (ORDER BY val DESC, id DESC)
FROM dbo.EvenRows
) AS x
WHERE ra BETWEEN rd - 1 AND rd + 1; 2005_B – Zeilennummer + Anzahl
Dieser ist dem obigen ziemlich ähnlich und verwendet eine einzige Berechnung von ROW_NUMBER() und dann mit dem Gesamtwert COUNT() um die "mittlere" ein oder zwei Zeilen zu finden:
SELECT @Median = AVG(1.0 * Val)
FROM
(
SELECT val,
c = COUNT(*) OVER (),
rn = ROW_NUMBER() OVER (ORDER BY val)
FROM dbo.EvenRows
) AS x
WHERE rn IN ((c + 1)/2, (c + 2)/2); 2005_C – Variation auf Zeilennummer + Anzahl
Kollege MVP Itzik Ben-Gan hat mir diese Methode gezeigt, die die gleiche Antwort wie die beiden oben genannten Methoden erzielt, aber auf eine ganz geringfügig andere Weise:
SELECT @Median = AVG(1.0 * val)
FROM
(
SELECT o.val, rn = ROW_NUMBER() OVER (ORDER BY o.val), c.c
FROM dbo.EvenRows AS o
CROSS JOIN (SELECT c = COUNT(*) FROM dbo.EvenRows) AS c
) AS x
WHERE rn IN ((c + 1)/2, (c + 2)/2);
SQL-Server 2012
In SQL Server 2012 verfügen wir über neue Fensterfunktionen in T-SQL, mit denen statistische Berechnungen wie Median direkter ausgedrückt werden können. Um den Median für eine Reihe von Werten zu berechnen, können wir PERCENTILE_CONT() verwenden . Wir können auch die neue "Paging"-Erweiterung für ORDER BY verwenden -Klausel (OFFSET / FETCH ).
2012_A – neue Verteilungsfunktionalität
Diese Lösung verwendet eine sehr einfache Berechnung mit Verteilung (wenn Sie bei einer geraden Anzahl von Zeilen nicht den Durchschnitt zwischen den beiden mittleren Werten wollen).
SELECT @Median = PERCENTILE_CONT(0.5) WITHIN GROUP (ORDER BY val) OVER () FROM dbo.EvenRows;
2012_B – Paging-Trick
Dieses Beispiel implementiert eine clevere Verwendung von OFFSET / FETCH (und nicht genau eine, für die es gedacht war) – wir bewegen uns einfach zu der Reihe, die vor der Hälfte der Zählung liegt, und nehmen dann die nächsten ein oder zwei Reihen, je nachdem, ob die Zählung gerade oder ungerade war. Danke an Itzik Ben-Gan für den Hinweis auf diesen Ansatz.
DECLARE @c BIGINT = (SELECT COUNT(*) FROM dbo.EvenRows);
SELECT AVG(1.0 * val)
FROM (
SELECT val FROM dbo.EvenRows
ORDER BY val
OFFSET (@c - 1) / 2 ROWS
FETCH NEXT 1 + (1 - @c % 2) ROWS ONLY
) AS x;
Aber welches ist besser?
Wir haben überprüft, dass die oben genannten Methoden alle die erwarteten Ergebnisse in unserer kleinen Tabelle liefern, und wir wissen, dass die SQL Server 2012-Version die sauberste und logischste Syntax hat. Aber welches sollten Sie in Ihrer geschäftigen Produktionsumgebung verwenden? Wir können eine viel größere Tabelle aus Systemmetadaten erstellen und sicherstellen, dass wir viele doppelte Werte haben. Dieses Skript erzeugt eine Tabelle mit 10.000.000 nicht eindeutigen Ganzzahlen:
USE tempdb; GO CREATE TABLE dbo.obj(id INT IDENTITY(1,1), val INT); CREATE CLUSTERED INDEX x ON dbo.obj(val, id); INSERT dbo.obj(val) SELECT TOP (10000000) o.[object_id] FROM sys.all_columns AS c CROSS JOIN sys.all_objects AS o CROSS JOIN sys.all_objects AS o2 WHERE o.[object_id] > 0 ORDER BY c.[object_id];
Auf meinem System sollte der Median für diese Tabelle 146.099.561 betragen. Ich kann dies ziemlich schnell ohne eine manuelle Stichprobe von 10.000.000 Zeilen berechnen, indem ich die folgende Abfrage verwende:
SELECT val FROM
(
SELECT val, rn = ROW_NUMBER() OVER (ORDER BY val)
FROM dbo.obj
) AS x
WHERE rn IN (4999999, 5000000, 5000001); Ergebnisse:
val rn ---- ---- 146099561 4999999 146099561 5000000 146099561 5000001
Jetzt können wir für jede Methode eine gespeicherte Prozedur erstellen, überprüfen, ob jede die richtige Ausgabe erzeugt, und dann Leistungsmetriken wie Dauer, CPU und Lesevorgänge messen. Wir führen alle diese Schritte mit der vorhandenen Tabelle durch und auch mit einer Kopie der Tabelle, die nicht vom Clustered-Index profitiert (wir löschen sie und erstellen die Tabelle als Heap neu).
Ich habe sieben Prozeduren erstellt, die die obigen Abfragemethoden implementieren. Der Kürze halber werde ich sie hier nicht auflisten, aber jeder trägt den Namen dbo.Median_<version> , z.B. dbo.Median_2000_A , dbo.Median_2000_B usw. entsprechend den oben beschriebenen Ansätzen. Wenn wir diese sieben Prozeduren mit dem kostenlosen SQL Sentry Plan Explorer ausführen, beobachten wir Folgendes in Bezug auf Dauer, CPU und Lesevorgänge (beachten Sie, dass wir DBCC FREEPROCCACHE und DBCC DROPCLEANBUFFERS zwischen den Ausführungen ausführen):
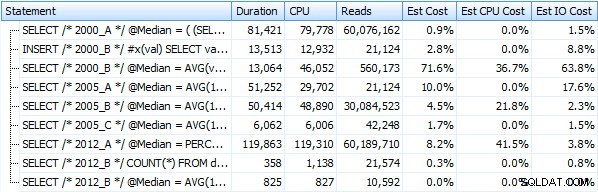
Und diese Metriken ändern sich überhaupt nicht, wenn wir stattdessen gegen einen Haufen arbeiten. Die größte prozentuale Änderung war die Methode, die am Ende immer noch die schnellste war:der Paging-Trick mit OFFSET / FETCH:
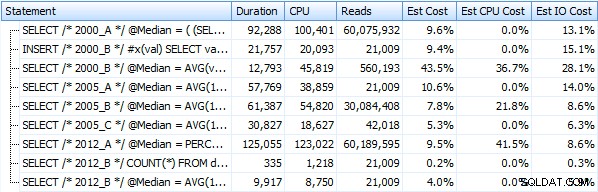
Hier ist eine grafische Darstellung der Ergebnisse. Um es deutlicher zu machen, habe ich den langsamsten Performer in Rot und den schnellsten Ansatz in Grün hervorgehoben.
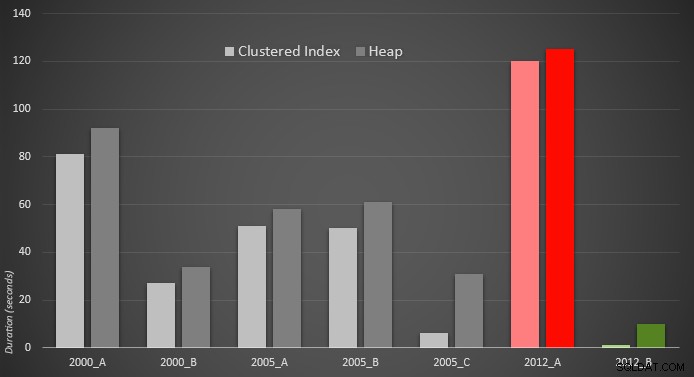
Ich war überrascht zu sehen, dass in beiden Fällen PERCENTILE_CONT() – die für diese Art der Berechnung konzipiert wurde – ist eigentlich schlechter als alle anderen früheren Lösungen. Ich denke, es zeigt nur, dass neuere Syntax zwar manchmal unsere Codierung einfacher macht, aber nicht immer garantiert, dass sich die Leistung verbessert. Ich war auch überrascht, OFFSET / FETCH zu sehen erweisen sich als so nützlich in Szenarien, die normalerweise nicht zu ihrem Zweck passen – Paginierung.
Auf jeden Fall hoffe ich, dass ich gezeigt habe, welchen Ansatz Sie verwenden sollten, abhängig von Ihrer Version von SQL Server (und dass die Wahl dieselbe sein sollte, ob Sie einen unterstützenden Index für die Berechnung haben oder nicht).