In Teil 5 meiner Serie über Tabellenausdrücke habe ich die folgende Lösung zum Generieren einer Reihe von Zahlen mithilfe von CTEs, einem Tabellenwertkonstruktor und Kreuzverknüpfungen bereitgestellt:
DECLARE @low AS BIGINT = 1001, @high AS BIGINT = 1010;
WITH
L0 AS ( SELECT 1 AS c FROM (VALUES(1),(1)) AS D(c) ),
L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
L4 AS ( SELECT 1 AS c FROM L3 AS A CROSS JOIN L3 AS B ),
L5 AS ( SELECT 1 AS c FROM L4 AS A CROSS JOIN L4 AS B ),
Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM L5 )
SELECT TOP(@high - @low + 1) @low + rownum - 1 AS n
FROM Nums
ORDER BY rownum; Es gibt viele praktische Anwendungsfälle für ein solches Tool, darunter das Generieren einer Reihe von Datums- und Uhrzeitwerten, das Erstellen von Beispieldaten und mehr. In Anbetracht des allgemeinen Bedarfs bieten einige Plattformen ein integriertes Tool, wie z. B. die generate_series-Funktion von PostgreSQL. Zum Zeitpunkt des Verfassens dieses Artikels bietet T-SQL kein solches integriertes Tool, aber man kann immer hoffen und dafür stimmen, dass ein solches Tool in Zukunft hinzugefügt wird.
In einem Kommentar zu meinem Artikel erwähnte Marcos Kirchner, dass er meine Lösung mit unterschiedlichen Tabellenwert-Konstruktorkardinalitäten getestet und unterschiedliche Ausführungszeiten für die verschiedenen Kardinalitäten erhalten habe.
Ich habe meine Lösung immer mit einer Basistabellenwert-Konstruktorkardinalität von 2 verwendet, aber der Kommentar von Marcos hat mich nachdenklich gemacht. Dieses Tool ist so nützlich, dass wir als Community unsere Kräfte bündeln sollten, um zu versuchen, die schnellste Version zu erstellen, die uns möglich ist. Das Testen verschiedener Basistabellenkardinalitäten ist nur eine Dimension, die Sie ausprobieren sollten. Es könnten noch viele andere sein. Ich werde die Leistungstests vorstellen, die ich mit meiner Lösung durchgeführt habe. Ich habe hauptsächlich mit verschiedenen Tabellenwert-Konstruktor-Kardinalitäten experimentiert, mit serieller versus paralleler Verarbeitung und mit Row-Mode versus Batch-Mode-Verarbeitung. Es könnte jedoch sein, dass eine ganz andere Lösung noch schneller ist als meine beste Version. Also, die Herausforderung ist eröffnet! Ich rufe alle Jedi, Padawan, Zauberer und Lehrlinge gleichermaßen an. Was ist die leistungsfähigste Lösung, die Sie herbeizaubern können? Haben Sie es in sich, die schnellste bisher gepostete Lösung zu schlagen? Wenn ja, teilen Sie Ihre als Kommentar zu diesem Artikel und verbessern Sie jede von anderen gepostete Lösung.
Anforderungen:
- Implementieren Sie Ihre Lösung als Inline-Tabellenwertfunktion (iTVF) namens dbo.GetNumsYourName mit den Parametern @low AS BIGINT und @high AS BIGINT. Sehen Sie sich als Beispiel die an, die ich am Ende dieses Artikels einreiche.
- Bei Bedarf können Sie unterstützende Tabellen in der Benutzerdatenbank erstellen.
- Sie können bei Bedarf Hinweise hinzufügen.
- Wie bereits erwähnt, sollte die Lösung Trennzeichen vom Typ BIGINT unterstützen, aber Sie können von einer maximalen Reihenkardinalität von 4.294.967.296 ausgehen.
- Um die Leistung Ihrer Lösung zu bewerten und mit anderen zu vergleichen, teste ich sie mit einem Bereich von 1 bis 100.000.000, wobei Ergebnisse nach Ausführung verwerfen in SSMS aktiviert sind.
Viel Glück für uns alle! Möge die beste Community gewinnen.;)
Unterschiedliche Kardinalitäten für Basistabellenwertkonstruktor
Ich habe mit unterschiedlichen Kardinalitäten des Basis-CTE experimentiert, beginnend mit 2 und fortschreitend in einer logarithmischen Skala, wobei die vorherige Kardinalität in jedem Schritt quadriert wurde:2, 4, 16 und 256.
Bevor Sie anfangen, mit verschiedenen Basiskardinalitäten zu experimentieren, könnte es hilfreich sein, eine Formel zu haben, die Ihnen bei gegebener Basiskardinalität und maximaler Bereichskardinalität mitteilt, wie viele Stufen von CTEs Sie benötigen. Als vorläufigen Schritt ist es einfacher, zunächst eine Formel zu entwickeln, die anhand der Basiskardinalität und der Anzahl der CTE-Stufen die maximale Kardinalität des resultierenden Bereichs berechnet. Hier ist eine solche Formel, ausgedrückt in T-SQL:
DECLARE @basecardinality AS INT = 2, @levels AS INT = 5; SELECT POWER(1.*@basecardinality, POWER(2., @levels));
Mit den obigen Beispiel-Eingabewerten ergibt dieser Ausdruck eine maximale Bereichskardinalität von 4.294.967.296.
Dann beinhaltet die umgekehrte Formel zur Berechnung der Anzahl der benötigten CTE-Stufen das Verschachteln von zwei Protokollfunktionen, etwa so:
DECLARE @basecardinality AS INT = 2, @seriescardinality AS BIGINT = 4294967296; SELECT CEILING(LOG(LOG(@seriescardinality, @basecardinality), 2));
Mit den obigen Beispieleingabewerten ergibt dieser Ausdruck 5. Beachten Sie, dass diese Zahl zusätzlich zum Basis-CTE steht, der den Tabellenwertkonstruktor hat, den ich in meiner Lösung L0 (für Ebene 0) genannt habe.
Frag mich nicht, wie ich zu diesen Formeln gekommen bin. Die Geschichte, an der ich festhalte, ist, dass Gandalf sie mir in meinen Träumen auf Elbisch gesagt hat.
Fahren wir mit dem Leistungstest fort. Stellen Sie sicher, dass Sie im Dialogfeld „SSMS-Abfrageoptionen“ unter „Raster“, „Ergebnisse“ die Option „Ergebnisse nach Ausführung verwerfen“ aktivieren. Verwenden Sie den folgenden Code, um einen Test mit einer Basis-CTE-Kardinalität von 2 auszuführen (erfordert 5 zusätzliche Ebenen von CTEs):
DECLARE @low AS BIGINT = 1, @high AS BIGINT = 100000000;
WITH
L0 AS ( SELECT 1 AS c FROM (VALUES(1),(1)) AS D(c) ),
L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
L4 AS ( SELECT 1 AS c FROM L3 AS A CROSS JOIN L3 AS B ),
L5 AS ( SELECT 1 AS c FROM L4 AS A CROSS JOIN L4 AS B ),
Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM L5 )
SELECT TOP(@high - @low + 1) @low + rownum - 1 AS n
FROM Nums
ORDER BY rownum; Ich habe den in Abbildung 1 gezeigten Plan für diese Hinrichtung erhalten.
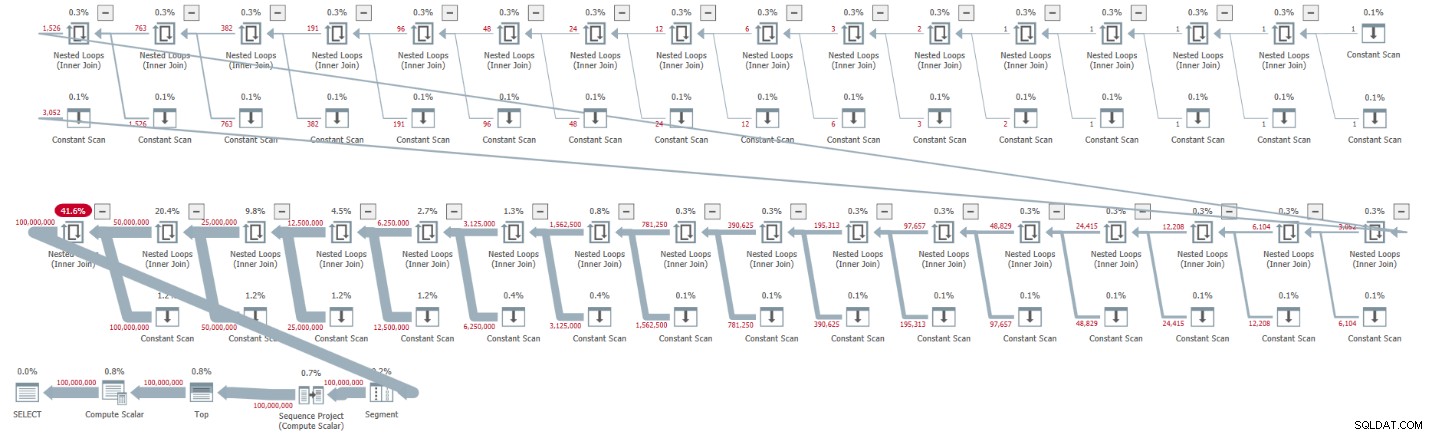Abbildung 1:Plan für Basis-CTE-Kardinalität von 2
Der Plan ist seriell, und alle Operatoren im Plan verwenden standardmäßig die Verarbeitung im Zeilenmodus. Wenn Sie standardmäßig einen parallelen Plan erhalten, z. B. wenn Sie die Lösung in ein iTVF kapseln und einen großen Bereich verwenden, erzwingen Sie vorerst einen seriellen Plan mit einem MAXDOP 1-Hinweis.
Beachten Sie, wie das Entpacken der CTEs zu 32 Instanzen des Constant Scan-Operators führte, die jeweils eine Tabelle mit zwei Zeilen darstellen.
Ich habe die folgenden Leistungsstatistiken für diese Ausführung:
CPU time = 30188 ms, elapsed time = 32844 ms.
Verwenden Sie den folgenden Code, um die Lösung mit einer Basis-CTE-Kardinalität von 4 zu testen, was gemäß unserer Formel vier Stufen von CTEs erfordert:
DECLARE @low AS BIGINT = 1, @high AS BIGINT = 100000000;
WITH
L0 AS ( SELECT 1 AS c FROM (VALUES(1),(1),(1),(1)) AS D(c) ),
L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
L4 AS ( SELECT 1 AS c FROM L3 AS A CROSS JOIN L3 AS B ),
Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM L4 )
SELECT TOP(@high - @low + 1) @low + rownum - 1 AS n
FROM Nums
ORDER BY rownum; Ich habe den in Abbildung 2 gezeigten Plan für diese Hinrichtung erhalten.
Abbildung 2:Plan für eine Basis-CTE-Kardinalität von 4
Das Entpacken der CTEs führte zu 16 Constant-Scan-Operatoren, die jeweils eine Tabelle mit 4 Zeilen darstellen.
Ich habe die folgenden Leistungsstatistiken für diese Ausführung:
CPU time = 23781 ms, elapsed time = 25435 ms.
Dies ist eine ordentliche Verbesserung von 22,5 Prozent gegenüber der vorherigen Lösung.
Bei der Untersuchung der für die Abfrage gemeldeten Wartestatistiken ist der dominante Wartetyp SOS_SCHEDULER_YIELD. Tatsächlich ist die Wartezahl im Vergleich zur ersten Lösung merkwürdigerweise um 22,8 Prozent gesunken (Wartezahl 15.280 gegenüber 19.800).
Verwenden Sie den folgenden Code, um die Lösung mit einer Basis-CTE-Kardinalität von 16 zu testen, was gemäß unserer Formel drei Stufen von CTEs erfordert:
DECLARE @low AS BIGINT = 1, @high AS BIGINT = 100000000;
WITH
L0 AS ( SELECT 1 AS c
FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1)) AS D(c) ),
L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM L3 )
SELECT TOP(@high - @low + 1) @low + rownum - 1 AS n
FROM Nums
ORDER BY rownum; Ich habe den in Abbildung 3 gezeigten Plan für diese Ausführung erhalten.
Abbildung 3:Plan für eine Basis-CTE-Kardinalität von 16
Diesmal führte das Entpacken der CTEs zu 8 Constant-Scan-Operatoren, die jeweils eine Tabelle mit 16 Zeilen darstellen.
Ich habe die folgenden Leistungsstatistiken für diese Ausführung:
CPU time = 22968 ms, elapsed time = 24409 ms.
Diese Lösung reduziert die verstrichene Zeit weiter, wenn auch nur um wenige zusätzliche Prozent, was einer Reduzierung von 25,7 Prozent im Vergleich zur ersten Lösung entspricht. Auch hier sinkt die Wartezahl des Wartetyps SOS_SCHEDULER_YIELD weiter (12.938).
Der nächste Test, der in unserer logarithmischen Skala voranschreitet, beinhaltet eine Basis-CTE-Kardinalität von 256. Es ist lang und hässlich, aber versuchen Sie es:
DECLARE @low AS BIGINT = 1, @high AS BIGINT = 100000000;
WITH
L0 AS ( SELECT 1 AS c
FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1)) AS D(c) ),
L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM L2 )
SELECT TOP(@high - @low + 1) @low + rownum - 1 AS n
FROM Nums
ORDER BY rownum; Ich habe den in Abbildung 4 gezeigten Plan für diese Hinrichtung erhalten.
Abbildung 4:Plan für eine Basis-CTE-Kardinalität von 256
Diesmal führte das Entpacken der CTEs zu nur vier Constant-Scan-Operatoren mit jeweils 256 Zeilen.
Ich habe die folgenden Leistungszahlen für diese Ausführung:
CPU time = 23516 ms, elapsed time = 25529 ms.
Diesmal scheint sich die Leistung im Vergleich zur vorherigen Lösung mit einer Basis-CTE-Kardinalität von 16 etwas verschlechtert zu haben. Tatsächlich hat sich die Wartezahl des Wartetyps SOS_SCHEDULER_YIELD etwas auf 13.176 erhöht. Es scheint also, als hätten wir unsere goldene Zahl gefunden – 16!
Parallele versus serielle Pläne
Ich habe damit experimentiert, einen parallelen Plan mit dem Hinweis ENABLE_PARALLEL_PLAN_PREFERENCE zu erzwingen, aber es hat die Leistung beeinträchtigt. Tatsächlich habe ich bei der Implementierung der Lösung als iTVF standardmäßig einen parallelen Plan für große Reichweiten auf meinem Computer erhalten und musste einen seriellen Plan mit einem MAXDOP 1-Hinweis erzwingen, um eine optimale Leistung zu erzielen.
Stapelverarbeitung
Die Hauptressource, die in den Plänen für meine Lösungen verwendet wird, ist die CPU. Da es bei der Stapelverarbeitung vor allem darum geht, die CPU-Effizienz zu verbessern, insbesondere wenn es um eine große Anzahl von Zeilen geht, lohnt es sich, diese Option auszuprobieren. Die Hauptaktivität hier, die von der Stapelverarbeitung profitieren kann, ist die Berechnung der Zeilennummer. Ich habe meine Lösungen in SQL Server 2019 Enterprise Edition getestet. SQL Server hat standardmäßig für alle zuvor gezeigten Lösungen die Verarbeitung im Zeilenmodus ausgewählt. Anscheinend hat diese Lösung die Heuristik nicht bestanden, die erforderlich ist, um den Batch-Modus im Rowstore zu aktivieren. Es gibt mehrere Möglichkeiten, SQL Server dazu zu bringen, hier die Stapelverarbeitung zu verwenden.
Option 1 besteht darin, eine Tabelle mit einem Columnstore-Index in die Lösung einzubeziehen. Sie können dies erreichen, indem Sie eine Dummy-Tabelle mit einem Columnstore-Index erstellen und einen Dummy-Left-Join in die äußerste Abfrage zwischen unserem Nums-CTE und dieser Tabelle einfügen. Hier ist die Dummy-Tabellendefinition:
CREATE TABLE dbo.BatchMe(col1 INT NOT NULL, INDEX idx_cs CLUSTERED COLUMNSTORE);
Überarbeiten Sie dann die äußere Abfrage gegen Nums, um FROM Nums LEFT OUTER JOIN dbo.BatchMe ON 1 =0 zu verwenden. Hier ist ein Beispiel mit einer Basis-CTE-Kardinalität von 16:
DECLARE @low AS BIGINT = 1, @high AS BIGINT = 100000000;
WITH
L0 AS ( SELECT 1 AS c
FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1)) AS D(c) ),
L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM L3 )
SELECT TOP(@high - @low + 1) @low + rownum - 1 AS n
FROM Nums LEFT OUTER JOIN dbo.BatchMe ON 1 = 0
ORDER BY rownum; Ich habe den in Abbildung 5 gezeigten Plan für diese Ausführung erhalten.
Abbildung 5:Plan mit Stapelverarbeitung
Beachten Sie die Verwendung des Window Aggregate-Operators im Stapelmodus zur Berechnung der Zeilennummern. Beachten Sie auch, dass der Plan den Dummy-Tisch nicht beinhaltet. Der Optimierer hat es optimiert.
Der Vorteil von Option 1 besteht darin, dass sie in allen SQL Server-Editionen funktioniert und in SQL Server 2016 oder höher relevant ist, da der Window Aggregate-Operator im Batchmodus in SQL Server 2016 eingeführt wurde. Der Nachteil besteht darin, dass die Dummy-Tabelle erstellt und eingeschlossen werden muss es in der Lösung.
Option 2, um Batch-Verarbeitung für unsere Lösung zu erhalten, sofern Sie SQL Server 2019 Enterprise Edition verwenden, besteht darin, den undokumentierten, selbsterklärenden Hinweis OVERRIDE_BATCH_MODE_HEURISTICS (Details im Artikel von Dmitry Pilugin) wie folgt zu verwenden:
DECLARE @low AS BIGINT = 1, @high AS BIGINT = 100000000;
WITH
L0 AS ( SELECT 1 AS c
FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1)) AS D(c) ),
L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM L3 )
SELECT TOP(@high - @low + 1) @low + rownum - 1 AS n
FROM Nums
ORDER BY rownum
OPTION(USE HINT('OVERRIDE_BATCH_MODE_HEURISTICS')); Der Vorteil von Option 2 ist, dass Sie keine Dummy-Tabelle erstellen und in Ihre Lösung einbeziehen müssen. Die Nachteile sind, dass Sie die Enterprise Edition verwenden müssen, mindestens SQL Server 2019 verwenden müssen, wo der Batchmodus auf Rowstore eingeführt wurde, und die Lösung die Verwendung eines undokumentierten Hinweises beinhaltet. Aus diesen Gründen bevorzuge ich Option 1.
Hier sind die Leistungszahlen, die ich für die verschiedenen Basis-CTE-Kardinalitäten erhalten habe:
Cardinality 2: CPU time = 21594 ms, elapsed time = 22743 ms (down from 32844). Cardinality 4: CPU time = 18375 ms, elapsed time = 19394 ms (down from 25435). Cardinality 16: CPU time = 17640 ms, elapsed time = 18568 ms (down from 24409). Cardinality 256: CPU time = 17109 ms, elapsed time = 18507 ms (down from 25529).
Abbildung 6 zeigt einen Leistungsvergleich zwischen den verschiedenen Lösungen:
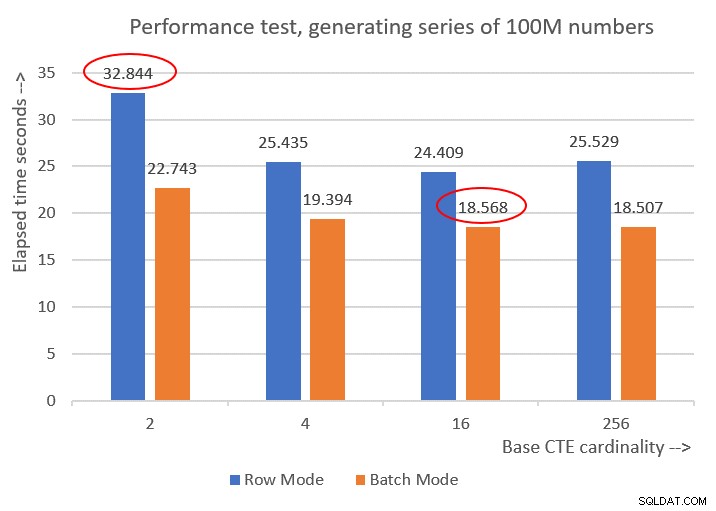Abbildung 6:Leistungsvergleich
Sie können eine anständige Leistungssteigerung von 20-30 Prozent gegenüber den Gegenstücken im Zeilenmodus beobachten.
Seltsamerweise schnitt bei der Verarbeitung im Stapelmodus die Lösung mit der Basis-CTE-Kardinalität von 256 am besten ab. Es ist jedoch nur ein kleines bisschen schneller als die Lösung mit einer Basis-CTE-Kardinalität von 16. Der Unterschied ist so gering, und letztere hat einen klaren Vorteil in Bezug auf die Codekürze, dass ich bei 16 bleiben würde.
Meine Optimierungsbemühungen führten also zu einer Verbesserung von 43,5 Prozent gegenüber der ursprünglichen Lösung mit der Basiskardinalität von 2 unter Verwendung der Zeilenmodusverarbeitung.
Die Herausforderung läuft!
Ich reiche zwei Lösungen als meinen Community-Beitrag zu dieser Herausforderung ein. Wenn Sie SQL Server 2016 oder höher ausführen und eine Tabelle in der Benutzerdatenbank erstellen können, erstellen Sie die folgende Dummy-Tabelle:
CREATE TABLE dbo.BatchMe(col1 INT NOT NULL, INDEX idx_cs CLUSTERED COLUMNSTORE);
Und verwenden Sie die folgende iTVF-Definition:
CREATE OR ALTER FUNCTION dbo.GetNumsItzikBatch(@low AS BIGINT, @high AS BIGINT)
RETURNS TABLE
AS
RETURN
WITH
L0 AS ( SELECT 1 AS c
FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1)) AS D(c) ),
L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM L3 )
SELECT TOP(@high - @low + 1) @low + rownum - 1 AS n
FROM Nums LEFT OUTER JOIN dbo.BatchMe ON 1 = 0
ORDER BY rownum;
GO Verwenden Sie zum Testen den folgenden Code (stellen Sie sicher, dass Ergebnisse nach Ausführung verwerfen aktiviert sind):
SELECT n FROM dbo.GetNumsItzikBatch(1, 100000000) OPTION(MAXDOP 1);
Dieser Code ist auf meinem Rechner in 18 Sekunden fertig.
Wenn Sie aus irgendeinem Grund die Anforderungen der Stapelverarbeitungslösung nicht erfüllen können, reiche ich die folgende Funktionsdefinition als meine zweite Lösung ein:
CREATE OR ALTER FUNCTION dbo.GetNumsItzik(@low AS BIGINT, @high AS BIGINT)
RETURNS TABLE
AS
RETURN
WITH
L0 AS ( SELECT 1 AS c
FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),
(1),(1),(1),(1),(1),(1),(1),(1)) AS D(c) ),
L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
FROM L3 )
SELECT TOP(@high - @low + 1) @low + rownum - 1 AS n
FROM Nums
ORDER BY rownum;
GO Verwenden Sie zum Testen den folgenden Code:
SELECT n FROM dbo.GetNumsItzik(1, 100000000) OPTION(MAXDOP 1);
Dieser Code ist auf meinem Computer in 24 Sekunden abgeschlossen.
Du bist dran!
