Lösungen für Herausforderungen beim Zahlenreihengenerator – Teil 5

Dies ist der fünfte und letzte Teil der Reihe, der Lösungen für die Herausforderung des Zahlenreihengenerators behandelt. In Teil 1, Teil 2, Teil 3 und Teil 4 habe ich reine T-SQL-Lösungen behandelt. Schon früh, als ich das Rätsel veröffentlichte, bemerkten mehrere Leute, dass die leistungsstärkste Lösung wahrscheinlich eine CLR-basierte sein würde. In diesem Artikel stellen wir diese intuitive Annahme auf die Probe. Insbesondere werde ich CLR-basierte Lösungen behandeln, die von Kamil Kosno und Adam Machanic veröffentlicht wurden.

Vielen Dank an Alan Burstein, Joe Obbish, Adam Machanic, Christopher Ford, Jeff Moden, Charlie, NoamGr, Kamil Kosno, Dave Mason, John Nelson #2, Ed Wagner, Michael Burbea und Paul White für das Teilen Ihrer Ideen und Kommentare.

Ich werde meine Tests in einer Datenbank namens testdb durchführen. Verwenden Sie den folgenden Code, um die Datenbank zu erstellen, falls sie nicht vorhanden ist, und um E/A- und Zeitstatistiken zu aktivieren:

-- DB and stats
SET NOCOUNT ON;
SET STATISTICS IO, TIME ON;
GO
 
IF DB_ID('testdb') IS NULL CREATE DATABASE testdb;
GO
 
USE testdb;
GO

Der Einfachheit halber werde ich die strenge CLR-Sicherheit deaktivieren und die Datenbank mit dem folgenden Code vertrauenswürdig machen:

-- Enable CLR, disable CLR strict security and make db trustworthy
EXEC sys.sp_configure 'show advanced settings', 1;
RECONFIGURE;
 
EXEC sys.sp_configure 'clr enabled', 1;
EXEC sys.sp_configure 'clr strict security', 0;
RECONFIGURE;
 
EXEC sys.sp_configure 'show advanced settings', 0;
RECONFIGURE;
 
ALTER DATABASE testdb SET TRUSTWORTHY ON; 
GO

Frühere Lösungen

Bevor ich auf die CLR-basierten Lösungen eingehe, lassen Sie uns kurz die Leistung von zwei der leistungsstärksten T-SQL-Lösungen überprüfen.

Die leistungsfähigste T-SQL-Lösung, die keine dauerhaften Basistabellen verwendete (außer der leeren Columnstore-Dummy-Tabelle, um die Stapelverarbeitung zu erhalten) und daher keine E/A-Vorgänge beinhaltete, war die in der Funktion dbo.GetNumsAlanCharlieItzikBatch implementierte. Ich habe diese Lösung in Teil 1 behandelt.

Hier ist der Code zum Erstellen der leeren Columnstore-Dummy-Tabelle, die von der Abfrage der Funktion verwendet wird:

DROP TABLE IF EXISTS dbo.BatchMe;
GO
 
CREATE TABLE dbo.BatchMe(col1 INT NOT NULL, INDEX idx_cs CLUSTERED COLUMNSTORE);
GO

Und hier ist der Code mit der Definition der Funktion:

CREATE OR ALTER FUNCTION dbo.GetNumsAlanCharlieItzikBatch(@low AS BIGINT = 1, @high AS BIGINT)
  RETURNS TABLE
AS
RETURN
  WITH
    L0 AS ( SELECT 1 AS c
            FROM (VALUES(1),(1),(1),(1),(1),(1),(1),(1),
                        (1),(1),(1),(1),(1),(1),(1),(1)) AS D(c) ),
    L1 AS ( SELECT 1 AS c FROM L0 AS A CROSS JOIN L0 AS B ),
    L2 AS ( SELECT 1 AS c FROM L1 AS A CROSS JOIN L1 AS B ),
    L3 AS ( SELECT 1 AS c FROM L2 AS A CROSS JOIN L2 AS B ),
    Nums AS ( SELECT ROW_NUMBER() OVER(ORDER BY (SELECT NULL)) AS rownum
              FROM L3 )
  SELECT TOP(@high - @low + 1)
     rownum AS rn,
     @high + 1 - rownum AS op,
     @low - 1 + rownum AS n
  FROM Nums LEFT OUTER JOIN dbo.BatchMe ON 1 = 0
  ORDER BY rownum;
GO

Lassen Sie uns zuerst die Funktion testen, die eine Reihe von 100 Millionen Zahlen anfordert, wobei das MAX-Aggregat auf Spalte n angewendet wird:

SELECT MAX(n) AS mx FROM dbo.GetNumsAlanCharlieItzikBatch(1, 100000000) OPTION(MAXDOP 1);

Erinnern Sie sich, diese Testtechnik vermeidet die Übertragung von 100 Millionen Zeilen an den Aufrufer und vermeidet auch den Aufwand im Zeilenmodus, der mit der Variablenzuweisung verbunden ist, wenn die Variablenzuweisungsmethode verwendet wird.

Hier sind die Zeitstatistiken, die ich für diesen Test auf meinem Computer erhalten habe:

Die Ausführung dieser Funktion erzeugt natürlich keine logischen Lesevorgänge.

Als nächstes testen wir es mit der Reihenfolge, indem wir die Variablenzuweisungstechnik verwenden:

DECLARE @n AS BIGINT;
 
SELECT @n = n FROM dbo.GetNumsAlanCharlieItzikBatch(1, 100000000) ORDER BY n OPTION(MAXDOP 1);

Ich habe die folgenden Zeitstatistiken für diese Hinrichtung:

Denken Sie daran, dass diese Funktion nicht zu einer Sortierung führt, wenn die nach n geordneten Daten angefordert werden. Sie erhalten grundsätzlich den gleichen Plan, unabhängig davon, ob Sie die bestellten Daten anfordern oder nicht. Wir können den größten Teil der zusätzlichen Zeit in diesem Test im Vergleich zum vorherigen auf die 100 Millionen Zeilenmodus-basierten Variablenzuweisungen zurückführen.

Die leistungsstärkste T-SQL-Lösung, die eine persistente Basistabelle verwendete und daher zu einigen E/A-Vorgängen führte, wenn auch nur sehr wenigen, war die Lösung von Paul White, die in der Funktion dbo.GetNums_SQLkiwi implementiert wurde. Ich habe diese Lösung in Teil 4 behandelt.

Hier ist Pauls Code, um sowohl die von der Funktion verwendete Columnstore-Tabelle als auch die Funktion selbst zu erstellen:

-- Helper columnstore table
DROP TABLE IF EXISTS dbo.CS;
 
-- 64K rows (enough for 4B rows when cross joined)
-- column 1 is always zero
-- column 2 is (1...65536)
SELECT
    -- type as integer NOT NULL
    -- (everything is normalized to 64 bits in columnstore/batch mode anyway)
    n1 = ISNULL(CONVERT(integer, 0), 0), 
    n2 = ISNULL(CONVERT(integer, N.rn), 0)
INTO dbo.CS
FROM 
(
    SELECT
        rn = ROW_NUMBER() OVER (ORDER BY @@SPID)
    FROM master.dbo.spt_values AS SV1
    CROSS JOIN master.dbo.spt_values AS SV2
    ORDER BY 
        rn ASC
        OFFSET 0 ROWS
        FETCH NEXT 65536 ROWS ONLY
) AS N;
 
-- Single compressed rowgroup of 65,536 rows
CREATE CLUSTERED COLUMNSTORE INDEX CCI 
ON dbo.CS 
WITH (MAXDOP = 1);
GO
 
-- The function
CREATE OR ALTER FUNCTION dbo.GetNums_SQLkiwi
(
    @low bigint = 1,
    @high bigint
)
RETURNS table 
AS
RETURN
    SELECT
        N.rn,
        n = @low - 1 + N.rn,
        op = @high + 1 - N.rn
    FROM
    (
        SELECT 
            -- Use @@TRANCOUNT instead of @@SPID if you like all your queries serial
            rn = ROW_NUMBER() OVER (ORDER BY @@SPID ASC)
        FROM dbo.CS AS N1
        JOIN dbo.CS AS N2
            -- Batch mode hash cross join
            -- Integer not null data type avoid hash probe residual
            -- This is always 0 = 0
            ON N2.n1 = N1.n1
        WHERE
            -- Try to avoid SQRT on negative numbers and enable simplification 
            -- to single constant scan if @low > @high (with literals)
            -- No start-up filters in batch mode
            @high >= @low
            -- Coarse filter:
            -- Limit each side of the cross join to SQRT(target number of rows)
            -- IIF avoids SQRT on negative numbers with parameters
            AND N1.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high >= @low, @high - @low + 1, 0)))))
            AND N2.n2 <= CONVERT(integer, CEILING(SQRT(CONVERT(float, IIF(@high >= @low, @high - @low + 1, 0)))))
    ) AS N
    WHERE
        -- Precise filter:
        -- Batch mode filter the limited cross join to the exact number of rows needed
        -- Avoids the optimizer introducing a row-mode Top with following row mode compute scalar
        @low - 2 + N.rn < @high;
GO

Lassen Sie es uns zuerst ohne Auftrag mit der Aggregattechnik testen, was zu einem All-Batch-Modus-Plan führt:

SELECT MAX(n) AS mx FROM dbo.GetNums_SQLkiwi(1, 100000000) OPTION(MAXDOP 1);

Ich habe die folgenden Zeit- und E/A-Statistiken für diese Ausführung:

Testen wir die Funktion mit der Reihenfolge unter Verwendung der Variablenzuweisungstechnik:

DECLARE @n AS BIGINT;
 
SELECT @n = n FROM dbo.GetNums_SQLkiwi(1, 100000000) ORDER BY n OPTION(MAXDOP 1);

Wie bei der vorherigen Lösung vermeidet auch diese Lösung eine explizite Sortierung im Plan und erhält daher den gleichen Plan, unabhängig davon, ob Sie die bestellten Daten anfordern oder nicht. Aber auch dieser Test bringt einen zusätzlichen Nachteil mit sich, hauptsächlich aufgrund der hier verwendeten Variablenzuweisungstechnik, was dazu führt, dass der Variablenzuweisungsteil im Plan im Zeilenmodus verarbeitet wird.

Hier sind die Zeit- und E/A-Statistiken, die ich für diese Ausführung erhalten habe:

CLR-Lösungen

Sowohl Kamil Kosno als auch Adam Machanic stellten zunächst eine einfache reine CLR-Lösung bereit und entwickelten später eine anspruchsvollere CLR+T-SQL-Kombination. Ich beginne mit Kamils ​​Lösungen und gehe dann auf Adams Lösungen ein.

Lösungen von Kamil Kosno

Hier ist der CLR-Code, der in Kamils ​​erster Lösung verwendet wurde, um eine Funktion namens GetNums_KamilKosno1 zu definieren:

using System;
using System.Data.SqlTypes;
using System.Collections;
public partial class GetNumsKamil1
{
    [Microsoft.SqlServer.Server.SqlFunction(FillRowMethodName = "GetNums_KamilKosno1_Fill", TableDefinition = "n BIGINT")]
    public static IEnumerator GetNums_KamilKosno1(SqlInt64 low, SqlInt64 high)
    {
        return (low.IsNull || high.IsNull) ? new GetNumsCS(0, 0) : new GetNumsCS(low.Value, high.Value);
    }
 
    public static void GetNums_KamilKosno1_Fill(Object o, out SqlInt64 n)
    {
        n = (long)o;
    }
 
    private class GetNumsCS : IEnumerator
    {
        public GetNumsCS(long from, long to)
        {
            _lowrange = from;
            _current = _lowrange - 1;
            _highrange = to;
        }
 
        public bool MoveNext()
        {
            _current += 1;
            if (_current > _highrange) return false;
            else return true;
        }
 
        public object Current
        {
            get
            {
 
                return _current;
            }
        }
 
        public void Reset()
        {
            _current = _lowrange - 1;
        }
 
        long _lowrange;
        long _current;
        long _highrange;
    }
}

Die Funktion akzeptiert zwei Eingaben namens low und high und gibt eine Tabelle mit einer BIGINT-Spalte namens n zurück. Die Funktion ist eine Streaming-Art, die eine Zeile mit der nächsten Nummer in der Reihe pro Zeilenanforderung von der aufrufenden Abfrage zurückgibt. Wie Sie sehen können, hat Kamil die formalisiertere Methode zum Implementieren der IEnumerator-Schnittstelle gewählt, die das Implementieren der Methoden MoveNext (bewegt den Enumerator vor, um die nächste Zeile zu erhalten), Current (ruft die Zeile an der aktuellen Enumeratorposition ab) und Reset (setzt den Zähler an seine Anfangsposition, die vor der ersten Zeile steht).

Die Variable, die die aktuelle Nummer in der Reihe enthält, heißt _current. Der Konstruktor setzt _current auf die untere Grenze des angeforderten Bereichs minus 1, und dasselbe gilt für die Reset-Methode. Die MoveNext-Methode erhöht _current um 1. Wenn _current dann größer als die Obergrenze des angeforderten Bereichs ist, gibt die Methode „false“ zurück, was bedeutet, dass sie nicht erneut aufgerufen wird. Andernfalls gibt es true zurück, was bedeutet, dass es erneut aufgerufen wird. Die Methode Current gibt natürlich _current zurück. Wie Sie sehen können, ziemlich einfache Logik.

Ich habe das Visual Studio-Projekt GetNumsKamil1 aufgerufen und dafür den Pfad C:\Temp\ verwendet. Hier ist der Code, den ich verwendet habe, um die Funktion in der testdb-Datenbank bereitzustellen:

DROP FUNCTION IF EXISTS dbo.GetNums_KamilKosno1;
 
DROP ASSEMBLY IF EXISTS GetNumsKamil1;
GO
 
CREATE ASSEMBLY GetNumsKamil1
  FROM 'C:\Temp\GetNumsKamil1\GetNumsKamil1\bin\Debug\GetNumsKamil1.dll';
GO
 
CREATE FUNCTION dbo.GetNums_KamilKosno1(@low AS BIGINT = 1, @high AS BIGINT)
  RETURNS TABLE(n BIGINT)
  ORDER(n)
  AS EXTERNAL NAME GetNumsKamil1.GetNumsKamil1.GetNums_KamilKosno1;
GO

Beachten Sie die Verwendung der ORDER-Klausel in der CREATE FUNCTION-Anweisung. Die Funktion gibt die Zeilen in n-Reihenfolge aus. Wenn also die Zeilen in n-Reihenfolge in den Plan aufgenommen werden müssen, weiß SQL Server basierend auf dieser Klausel, dass eine Sortierung im Plan vermieden werden kann.

Lassen Sie uns die Funktion testen, zuerst mit der Aggregattechnik, wenn eine Bestellung nicht erforderlich ist:

SELECT MAX(n) AS mx FROM dbo.GetNums_KamilKosno1(1, 100000000);

Ich habe den in Abbildung 1 gezeigten Plan erhalten.

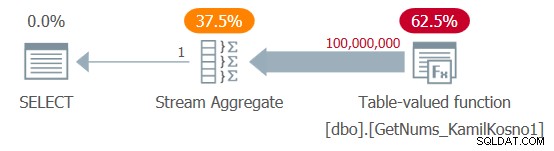Abbildung 1:Plan für die Funktion dbo.GetNums_KamilKosno1

Zu diesem Plan gibt es nicht viel zu sagen, außer der Tatsache, dass alle Operatoren den Zeilenausführungsmodus verwenden.

Ich habe die folgenden Zeitstatistiken für diese Hinrichtung:

Und natürlich waren keine logischen Lesevorgänge beteiligt.

Lassen Sie uns die Funktion mit der Reihenfolge testen, indem wir die Variablenzuweisungstechnik verwenden:

DECLARE @n AS BIGINT;
 
SELECT @n = n FROM dbo.GetNums_KamilKosno1(1, 100000000) ORDER BY n;

Ich habe den in Abbildung 2 gezeigten Plan für diese Hinrichtung erhalten.

Abbildung 2:Plan für die Funktion dbo.GetNums_KamilKosno1 mit ORDER BY

Beachten Sie, dass der Plan keine Sortierung enthält, da die Funktion mit der ORDER(n)-Klausel erstellt wurde. Es ist jedoch ein gewisser Aufwand erforderlich, um sicherzustellen, dass die Zeilen tatsächlich in der versprochenen Reihenfolge von der Funktion ausgegeben werden. Dies erfolgt mithilfe der Segment- und Sequence-Projektoperatoren, die zum Berechnen von Zeilennummern verwendet werden, und des Assert-Operators, der die Abfrageausführung abbricht, wenn der Test fehlschlägt. Diese Arbeit hat eine lineare Skalierung – anders als die n log n-Skalierung, die Sie erhalten hätten, wenn eine Sortierung erforderlich gewesen wäre –, aber sie ist immer noch nicht billig. Ich habe die folgenden Zeitstatistiken für diesen Test:

Die Ergebnisse könnten für einige überraschend sein – insbesondere für diejenigen, die intuitiv davon ausgegangen sind, dass die CLR-basierten Lösungen eine bessere Leistung erbringen würden als die T-SQL-Lösungen. Wie Sie sehen können, sind die Ausführungszeiten um eine Größenordnung länger als bei unserer leistungsstärksten T-SQL-Lösung.

Kamils ​​zweite Lösung ist ein CLR-T-SQL-Hybrid. Neben den niedrigen und hohen Eingaben fügt die CLR-Funktion (GetNums_KamilKosno2) eine schrittweise Eingabe hinzu und gibt Werte zwischen niedrig und hoch zurück, die einen Schritt voneinander entfernt sind. Hier ist der CLR-Code, den Kamil in seiner zweiten Lösung verwendet hat:

using System;
using System.Data.SqlTypes;
using System.Collections;
 
public partial class GetNumsKamil2
{
    [Microsoft.SqlServer.Server.SqlFunction(DataAccess = Microsoft.SqlServer.Server.DataAccessKind.None, IsDeterministic = true, IsPrecise = true, FillRowMethodName = "GetNums_Fill", TableDefinition = "n BIGINT")]
 
    public static IEnumerator GetNums_KamilKosno2(SqlInt64 low, SqlInt64 high, SqlInt64 step)
    {
        return (low.IsNull || high.IsNull) ? new GetNumsCS(0, 0, step.Value) : new GetNumsCS(low.Value, high.Value, step.Value);
    }
 
    public static void GetNums_Fill(Object o, out SqlInt64 n)
    {
        n = (long)o;
    }
 
    private class GetNumsCS : IEnumerator
    {
        public GetNumsCS(long from, long to, long step)
        {
            _lowrange = from;
            _step = step;
            _current = _lowrange - _step;
            _highrange = to;
        }
 
        public bool MoveNext()
        {
            _current = _current + _step;
            if (_current > _highrange) return false;
            else return true;
        }
 
        public object Current
        {
            get
            {
                return _current;
            }
        }
 
        public void Reset()
        {
            _current = _lowrange - _step;
        }
 
        long _lowrange;
        long _current;
        long _highrange;
        long _step;
    }
}

Ich habe das VS-Projekt GetNumsKamil2 genannt, es ebenfalls im Pfad C:\Temp\ platziert und den folgenden Code verwendet, um es in der testdb-Datenbank bereitzustellen:

-- Create assembly and function
DROP FUNCTION IF EXISTS dbo.GetNums_KamilKosno2;
DROP ASSEMBLY IF EXISTS GetNumsKamil2;
GO
 
CREATE ASSEMBLY GetNumsKamil2
  FROM 'C:\Temp\GetNumsKamil2\GetNumsKamil2\bin\Debug\GetNumsKamil2.dll';
GO
 
CREATE FUNCTION dbo.GetNums_KamilKosno2
    (@low AS BIGINT = 1, @high AS BIGINT, @step AS BIGINT)
  RETURNS TABLE(n BIGINT)
  ORDER(n)
  AS EXTERNAL NAME GetNumsKamil2.GetNumsKamil2.GetNums_KamilKosno2;
GO

Als Beispiel für die Verwendung der Funktion ist hier eine Anfrage, um Werte zwischen 5 und 59 mit einer Schrittweite von 10 zu generieren:

SELECT n FROM dbo.GetNums_KamilKosno2(5, 59, 10);

Dieser Code generiert die folgende Ausgabe:

n
---
5
15
25
35
45
55

Für den T-SQL-Teil verwendete Kamil eine Funktion namens dbo.GetNums_Hybrid_Kamil2 mit folgendem Code:

CREATE OR ALTER FUNCTION dbo.GetNums_Hybrid_Kamil2(@low AS BIGINT, @high AS BIGINT)
  RETURNS TABLE
AS
RETURN
  SELECT TOP (@high - @low + 1) V.n
  FROM dbo.GetNums_KamilKosno2(@low, @high, 10) AS GN
    CROSS APPLY (VALUES(0+GN.n),(1+GN.n),(2+GN.n),(3+GN.n),(4+GN.n),
                       (5+GN.n),(6+GN.n),(7+GN.n),(8+GN.n),(9+GN.n)) AS V(n);
GO

Wie Sie sehen können, ruft die T-SQL-Funktion die CLR-Funktion mit denselben @low- und @high-Eingaben auf, die sie erhält, und verwendet in diesem Beispiel eine Schrittweite von 10. Die Abfrage verwendet CROSS APPLY zwischen dem Ergebnis der CLR-Funktion und a Tabellenwertkonstruktor, der die endgültigen Zahlen generiert, indem er am Anfang des Schritts Werte im Bereich von 0 bis 9 hinzufügt. Der TOP-Filter wird verwendet, um sicherzustellen, dass Sie nicht mehr als die von Ihnen angeforderte Anzahl von Nummern erhalten.

Wichtig: Ich sollte betonen, dass Kamil hier davon ausgeht, dass der TOP-Filter basierend auf der Reihenfolge der Ergebnisnummern angewendet wird, was nicht wirklich garantiert ist, da die Abfrage keine ORDER BY-Klausel hat. Wenn Sie entweder eine ORDER BY-Klausel hinzufügen, um TOP zu unterstützen, oder TOP durch einen WHERE-Filter ersetzen, um einen deterministischen Filter zu gewährleisten, könnte dies das Leistungsprofil der Lösung vollständig ändern.

Testen wir jedenfalls zunächst die Funktion ohne Reihenfolge mit der Aggregattechnik:

SELECT MAX(n) AS mx FROM dbo.GetNums_Hybrid_Kamil2(1, 100000000);

Ich habe den in Abbildung 3 gezeigten Plan für diese Ausführung erhalten.

Abbildung 3:Plan für die Funktion dbo.GetNums_Hybrid_Kamil2

Auch hier verwenden alle Operatoren im Plan den Zeilenausführungsmodus.

Ich habe die folgenden Zeitstatistiken für diese Hinrichtung:

Und natürlich keine logischen Lesevorgänge.

Testen wir die Funktion mit order:

DECLARE @n AS BIGINT;
 
SELECT @n = n FROM dbo.GetNums_Hybrid_Kamil2(1, 100000000) ORDER BY n;

Ich habe den in Abbildung 4 gezeigten Plan erhalten.

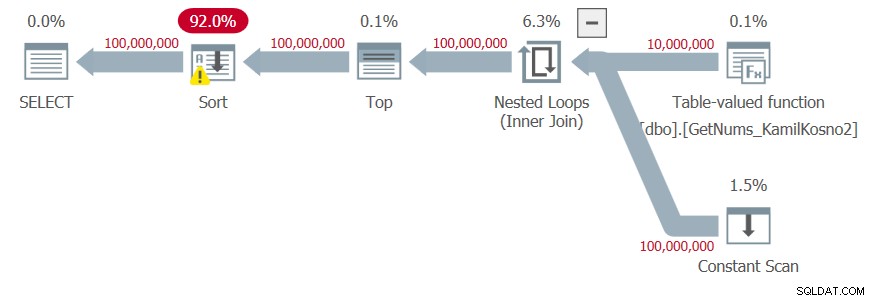Abbildung 4:Plan für die Funktion dbo.GetNums_Hybrid_Kamil2 mit ORDER BY

Da die Ergebniszahlen das Ergebnis der Manipulation der unteren Grenze des von der CLR-Funktion zurückgegebenen Schritts und des im Tabellenwertkonstruktor hinzugefügten Deltas sind, vertraut der Optimierer nicht darauf, dass die Ergebniszahlen in der angeforderten Reihenfolge generiert werden, und fügt dem Plan eine explizite Sortierung hinzu.

Ich habe die folgenden Zeitstatistiken für diese Hinrichtung:

Es scheint also, dass Kamils ​​zweite Lösung besser abschneidet als seine erste, wenn keine Bestellung erforderlich ist. Aber wenn Ordnung gefragt ist, ist es umgekehrt. In jedem Fall sind die T-SQL-Lösungen schneller. Ich persönlich würde der ersten Lösung vertrauen, aber nicht der zweiten.

Lösungen von Adam Machanic

Adams erste Lösung ist auch eine grundlegende CLR-Funktion, die einen Zähler kontinuierlich erhöht. Nur anstatt den komplizierteren formalisierten Ansatz zu verwenden, wie es Kamil getan hat, hat Adam einen einfacheren Ansatz verwendet, der den yield-Befehl pro Zeile aufruft, die zurückgegeben werden muss.

Hier ist Adams CLR-Code für seine erste Lösung, die eine Streaming-Funktion namens GetNums_AdamMachanic1 definiert:

using System.Data.SqlTypes;
using System.Collections;
 
public partial class GetNumsAdam1
{
    [Microsoft.SqlServer.Server.SqlFunction(
        FillRowMethodName = "GetNums_AdamMachanic1_fill",
        TableDefinition = "n BIGINT")]
 
    public static IEnumerable GetNums_AdamMachanic1(SqlInt64 min, SqlInt64 max)
    {
        var min_int = min.Value;
        var max_int = max.Value;
        for (; min_int <= max_int; min_int++)
        {
            yield return (min_int);
        }
    }
 
    public static void GetNums_AdamMachanic1_fill(object o, out long i)
    {
        i = (long)o;
    }
};

Die Lösung ist so elegant in ihrer Einfachheit. Wie Sie sehen können, akzeptiert die Funktion zwei Eingaben namens min und max, die die unteren und oberen Grenzpunkte des angeforderten Bereichs darstellen, und gibt eine Tabelle mit einer BIGINT-Spalte namens n zurück. Die Funktion initialisiert die Variablen min_int und max_int mit den Eingabeparameterwerten der jeweiligen Funktion. Die Funktion durchläuft dann eine Schleife solange min_int <=max_int, die bei jeder Iteration eine Zeile mit dem aktuellen Wert von min_int ergibt und min_int um 1 erhöht. Das war's.

Ich habe das Projekt GetNumsAdam1 in VS genannt, es in C:\Temp\ abgelegt und den folgenden Code verwendet, um es bereitzustellen:

-- Create assembly and function
DROP FUNCTION IF EXISTS dbo.GetNums_AdamMachanic1;
DROP ASSEMBLY IF EXISTS GetNumsAdam1;
GO
 
CREATE ASSEMBLY GetNumsAdam1
  FROM 'C:\Temp\GetNumsAdam1\GetNumsAdam1\bin\Debug\GetNumsAdam1.dll';
GO
 
CREATE FUNCTION dbo.GetNums_AdamMachanic1(@low AS BIGINT = 1, @high AS BIGINT)
  RETURNS TABLE(n BIGINT)
  ORDER(n)
  AS EXTERNAL NAME GetNumsAdam1.GetNumsAdam1.GetNums_AdamMachanic1;
GO

Ich habe den folgenden Code verwendet, um es mit der Aggregattechnik zu testen, für Fälle, in denen die Reihenfolge keine Rolle spielt:

SELECT MAX(n) AS mx FROM dbo.GetNums_AdamMachanic1(1, 100000000);

Ich habe den in Abbildung 5 gezeigten Plan für diese Ausführung erhalten.

Abbildung 5:Plan für die Funktion dbo.GetNums_AdamMachanic1

Der Plan ist dem Plan, den Sie zuvor für Kamils ​​erste Lösung gesehen haben, sehr ähnlich, und das Gleiche gilt für seine Leistung. Ich habe die folgenden Zeitstatistiken für diese Hinrichtung:

Und natürlich waren keine logischen Lesevorgänge erforderlich.

Lassen Sie uns die Funktion mit der Reihenfolge testen, indem wir die Variablenzuweisungstechnik verwenden:

DECLARE @n AS BIGINT;
 
SELECT @n = n FROM dbo.GetNums_AdamMachanic1(1, 100000000) ORDER BY n;

Ich habe den in Abbildung 6 gezeigten Plan für diese Ausführung erhalten.

Abbildung 6:Plan für die Funktion dbo.GetNums_AdamMachanic1 mit ORDER BY

Auch hier sieht der Plan ähnlich aus wie zuvor für Kamils ​​erste Lösung. Es war keine explizite Sortierung erforderlich, da die Funktion mit der ORDER-Klausel erstellt wurde, aber der Plan beinhaltet einige Arbeiten, um zu überprüfen, ob die Zeilen tatsächlich wie versprochen in der richtigen Reihenfolge zurückgegeben werden.

Ich habe die folgenden Zeitstatistiken für diese Hinrichtung:

In seiner zweiten Lösung kombinierte Adam auch einen CLR-Teil und einen T-SQL-Teil. Hier ist Adams Beschreibung der Logik, die er in seiner Lösung verwendet hat:

CLR ist eine gute Antwort für den zweiten Teil, wird aber natürlich durch die erste Ausgabe behindert. Als Kompromiss habe ich also ein T-SQL-TVF [namens GetNums_AdamMachanic2_8192] erstellt, das mit den Werten von 1 bis 8192 hartcodiert ist. (Ziemlich willkürliche Auswahl, aber zu groß und die QO beginnt ein wenig daran zu ersticken.) Als nächstes habe ich meine CLR-Funktion modifiziert [ mit dem Namen GetNums_AdamMachanic2_8192_base], um zwei Spalten auszugeben, "max_base" und "base_add", und ließ es Zeilen ausgeben wie:

max_base, base_add
——————
8191, 1
8192, 8192
8192, 16384
…
8192, 99991552
257, 99999744

Jetzt ist es eine einfache Schleife. Die CLR-Ausgabe wird an das T-SQL-TVF gesendet, das so eingerichtet ist, dass es nur bis zu „max_base“-Zeilen seines fest codierten Satzes zurückgibt. Und für jede Zeile fügt es "base_add" zum Wert hinzu, wodurch die erforderlichen Zahlen generiert werden. Der Schlüssel hier ist meiner Meinung nach, dass wir N Zeilen mit nur einem einzigen logischen Cross Join generieren können und die CLR-Funktion nur 1/8192 so viele Zeilen zurückgeben muss, dass sie schnell genug ist, um als Basisgenerator zu fungieren.“

Die Logik scheint ziemlich einfach zu sein.

Hier ist der Code, der verwendet wird, um die CLR-Funktion namens GetNums_AdamMachanic2_8192_base zu definieren:

using System.Data.SqlTypes;
using System.Collections;
 
public partial class GetNumsAdam2
{
    private struct row
    {
        public long max_base;
        public long base_add;
    }
 
    [Microsoft.SqlServer.Server.SqlFunction(
        FillRowMethodName = "GetNums_AdamMachanic2_8192_base_fill",
        TableDefinition = "max_base int, base_add int")]
 
    public static IEnumerable GetNums_AdamMachanic2_8192_base(SqlInt64 min, SqlInt64 max)
    {
        var min_int = min.Value;
        var max_int = max.Value;
        var min_group = min_int / 8192;
        var max_group = max_int / 8192;
 
        for (; min_group <= max_group; min_group++)
        {
            if (min_int > max_int)
                yield break;
            var max_base = 8192 - (min_int % 8192);
            if (min_group == max_group && max_int < (((max_int / 8192) + 1) * 8192) - 1)
                max_base = max_int - min_int + 1;
            yield return (
                new row()
                {
                    max_base = max_base,
                    base_add = min_int
                }
            );
            min_int = (min_group + 1) * 8192;
        }
    }
 
    public static void GetNums_AdamMachanic2_8192_base_fill(object o, out long max_base, out long base_add)
    {
        var r = (row)o;
        max_base = r.max_base;
        base_add = r.base_add;
    }
};

Ich habe das VS-Projekt GetNumsAdam2 genannt und wie bei den anderen Projekten im Pfad C:\Temp\ abgelegt. Hier ist der Code, den ich verwendet habe, um die Funktion in der testdb-Datenbank bereitzustellen:

-- Create assembly and function
DROP FUNCTION IF EXISTS dbo.GetNums_AdamMachanic2_8192_base;
DROP ASSEMBLY IF EXISTS GetNumsAdam2;
GO
 
CREATE ASSEMBLY GetNumsAdam2
  FROM 'C:\Temp\GetNumsAdam2\GetNumsAdam2\bin\Debug\GetNumsAdam2.dll';
GO
 
CREATE FUNCTION dbo.GetNums_AdamMachanic2_8192_base(@max_base AS BIGINT, @add_base AS BIGINT)
  RETURNS TABLE(max_base BIGINT, base_add BIGINT)
  ORDER(base_add)
  AS EXTERNAL NAME GetNumsAdam2.GetNumsAdam2.GetNums_AdamMachanic2_8192_base;
GO

Hier ist ein Beispiel für die Verwendung von GetNums_AdamMachanic2_8192_base mit dem Bereich von 1 bis 100 M:

SELECT * FROM dbo.GetNums_AdamMachanic2_8192_base(1, 100000000);

Dieser Code erzeugt die folgende Ausgabe, hier in abgekürzter Form dargestellt:

max_base             base_add
-------------------- --------------------
8191                 1
8192                 8192
8192                 16384
8192                 24576
8192                 32768
...
8192                 99966976
8192                 99975168
8192                 99983360
8192                 99991552
257                  99999744

(12208 rows affected)

Hier ist der Code mit der Definition der T-SQL-Funktion GetNums_AdamMachanic2_8192 (abgekürzt):

CREATE OR ALTER FUNCTION dbo.GetNums_AdamMachanic2_8192(@max_base AS BIGINT, @add_base AS BIGINT)
  RETURNS TABLE
AS
RETURN
  SELECT TOP (@max_base) V.i + @add_base AS val
  FROM (
    VALUES
    (0),
    (1),
    (2),
    (3),
    (4),
    ...
    (8187),
    (8188),
    (8189),
    (8190),
    (8191)
  ) AS V(i);
GO

Wichtig: Auch hier sollte ich betonen, dass Adam ähnlich wie bei Kamils ​​zweiter Lösung davon ausgeht, dass der TOP-Filter die obersten Zeilen basierend auf der Reihenfolge des Zeilenauftretens im Tabellenwertkonstruktor extrahiert, was nicht wirklich garantiert ist. Wenn Sie eine ORDER BY-Klausel hinzufügen, um TOP zu unterstützen, oder den Filter in einen WHERE-Filter ändern, erhalten Sie einen deterministischen Filter, aber dies kann das Leistungsprofil der Lösung vollständig ändern.

Schließlich ist hier die äußerste T-SQL-Funktion, dbo.GetNums_AdamMachanic2, die der Endbenutzer aufruft, um die Zahlenreihe zu erhalten:

CREATE OR ALTER FUNCTION dbo.GetNums_AdamMachanic2(@low AS BIGINT = 1, @high AS BIGINT)
  RETURNS TABLE
AS
RETURN
  SELECT Y.val AS n
  FROM ( SELECT max_base, base_add
  	     FROM dbo.GetNums_AdamMachanic2_8192_base(@low, @high) ) AS X
    CROSS APPLY dbo.GetNums_AdamMachanic2_8192(X.max_base, X.base_add) AS Y
GO

Diese Funktion verwendet den CROSS APPLY-Operator, um die innere T-SQL-Funktion dbo.GetNums_AdamMachanic2_8192 pro Zeile anzuwenden, die von der inneren CLR-Funktion dbo.GetNums_AdamMachanic2_8192_base.

Lassen Sie uns diese Lösung zuerst mit der Aggregattechnik testen, wenn die Reihenfolge keine Rolle spielt:

SELECT MAX(n) AS mx FROM dbo.GetNums_AdamMachanic2(1, 100000000);

Ich habe den in Abbildung 7 gezeigten Plan für diese Hinrichtung erhalten.

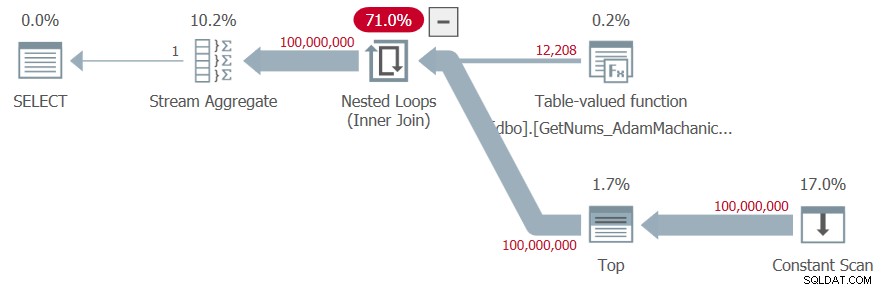Abbildung 7:Plan für die Funktion dbo.GetNums_AdamMachanic2

Ich habe die folgenden Zeitstatistiken für diesen Test:

Es waren keine logischen Lesevorgänge erforderlich.

Die Ausführungszeit ist nicht schlecht, aber beachten Sie die hohe Kompilierzeit aufgrund des großen verwendeten Tabellenwertkonstruktors. Sie würden unabhängig von der angeforderten Bereichsgröße eine so hohe Kompilierzeit zahlen, daher ist dies besonders schwierig, wenn Sie die Funktion mit sehr kleinen Bereichen verwenden. Und diese Lösung ist immer noch langsamer als die T-SQL-Lösungen.

Testen wir die Funktion mit order:

DECLARE @n AS BIGINT;
 
SELECT @n = n FROM dbo.GetNums_AdamMachanic2(1, 100000000) ORDER BY n;

Ich habe den in Abbildung 8 gezeigten Plan für diese Hinrichtung erhalten.

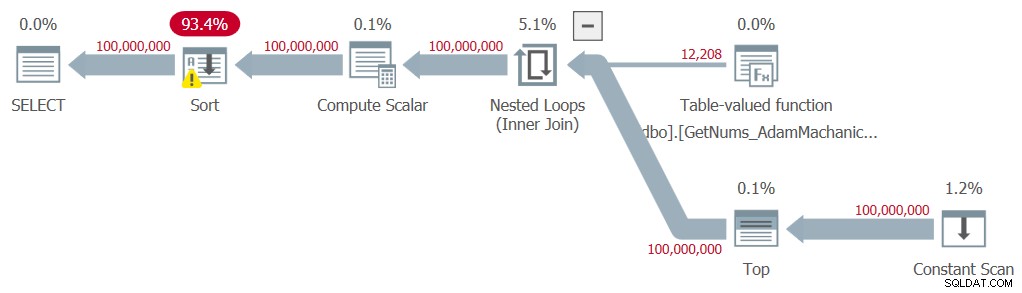Abbildung 8:Plan für die Funktion dbo.GetNums_AdamMachanic2 mit ORDER BY

Wie bei der zweiten Lösung von Kamil ist eine explizite Sortierung im Plan erforderlich, was zu einer erheblichen Leistungseinbuße führt. Hier sind die Zeitstatistiken, die ich für diesen Test erhalten habe:

Außerdem gibt es immer noch die hohe Kompilierzeitstrafe von etwa einer Drittelsekunde.

Schlussfolgerung

Es war interessant, CLR-basierte Lösungen für die Zahlenserienherausforderung zu testen, da viele Leute zunächst davon ausgingen, dass die leistungsstärkste Lösung wahrscheinlich eine CLR-basierte sein wird. Kamil und Adam verwendeten ähnliche Ansätze, wobei der erste Versuch eine einfache Schleife verwendete, die einen Zähler erhöht und eine Zeile mit dem nächsten Wert pro Iteration liefert, und der anspruchsvollere zweite Versuch, der CLR- und T-SQL-Teile kombiniert. Persönlich fühle ich mich nicht wohl mit der Tatsache, dass sie sich sowohl in Kamils ​​als auch in Adams zweiten Lösungen auf einen nichtdeterministischen TOP-Filter stützten, und als ich ihn in meinen eigenen Tests in einen deterministischen umwandelte, hatte dies einen negativen Einfluss auf die Leistung der Lösung . Either way, our two T-SQL solutions perform better than the CLR ones, and do not result in explicit sorting in the plan when you need the rows ordered. So I don’t really see the value in pursuing the CLR route any further. Figure 9 has a performance summary of the solutions that I presented in this article.

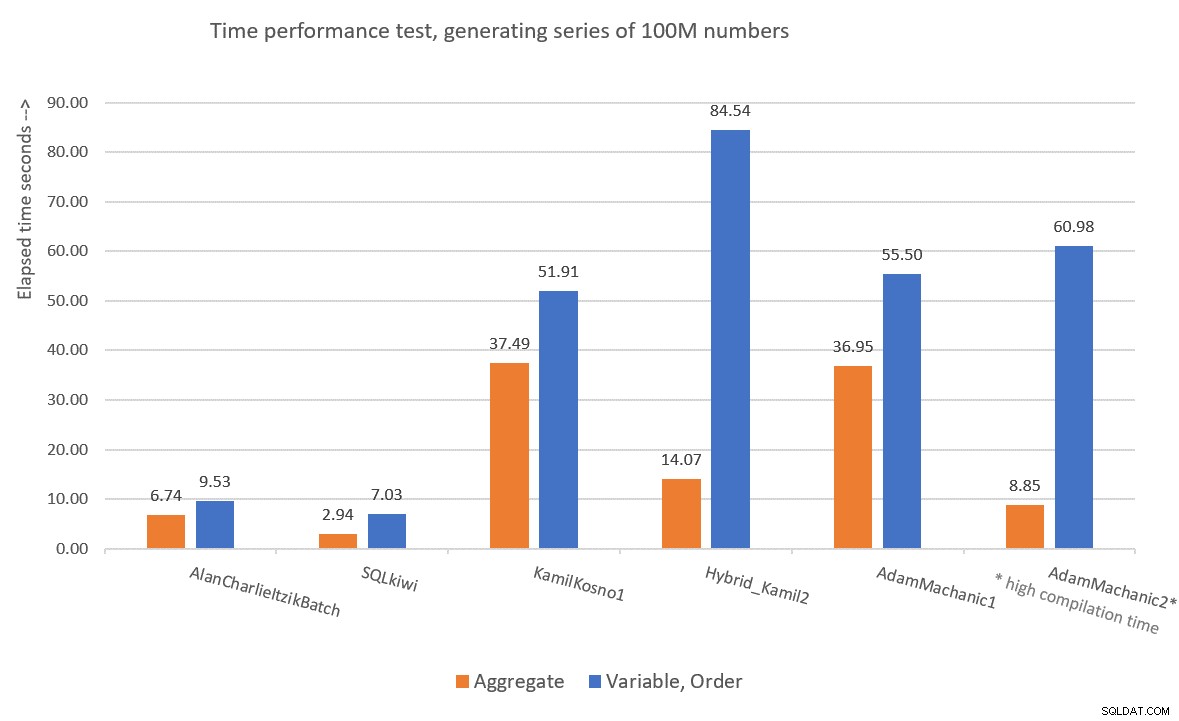Figure 9:Time performance comparison

To me, GetNums_AlanCharlieItzikBatch should be the solution of choice when you require absolutely no I/O footprint, and GetNums_SQKWiki should be preferred when you don’t mind a small I/O footprint. Of course, we can always hope that one day Microsoft will add this critically useful tool as a built-in one, and hopefully if/when they do, it will be a performant solution that supports batch processing and parallelism. So don’t forget to vote for this feature improvement request, and maybe even add your comments for why it’s important for you.

I really enjoyed working on this series. I learned a lot during the process, and hope that you did too.