Dieser Artikel befasst sich mit der Selektivitäts- und Kardinalitätsschätzung für Prädikate auf COUNT(*) Ausdrücke, wie in HAVING zu sehen ist Klauseln. Die Details sind für sich hoffentlich interessant. Sie bieten auch einen Einblick in einige der allgemeinen Ansätze und Algorithmen, die vom Kardinalitätsschätzer verwendet werden.
Ein einfaches Beispiel mit der AdventureWorks-Beispieldatenbank:
SELECT A.City FROM Person.[Address] AS A GROUP BY A.City HAVING COUNT_BIG(*) = 1;
Uns interessiert, wie SQL Server eine Schätzung für das Prädikat des Zählausdrucks in HAVING ableitet Klausel.
Natürlich das HAVING -Klausel ist nur Syntaxzucker. Wir hätten die Abfrage auch mit einer abgeleiteten Tabelle oder einem allgemeinen Tabellenausdruck schreiben können:
-- Derived table
SELECT SQ1.City
FROM
(
SELECT A.City, Expr1001 = COUNT_BIG(*)
FROM Person.[Address] AS A
GROUP BY A.City
) AS SQ1
WHERE SQ1.Expr1001 = 1;
-- CTE
WITH Grouped AS
(
SELECT A.City, Expr1001 = COUNT_BIG(*)
FROM Person.[Address] AS A
GROUP BY A.City
)
SELECT G.City
FROM Grouped AS G
WHERE G.Expr1001 = 1; Alle drei Abfrageformen erzeugen denselben Ausführungsplan mit identischen Abfrageplan-Hashwerten.
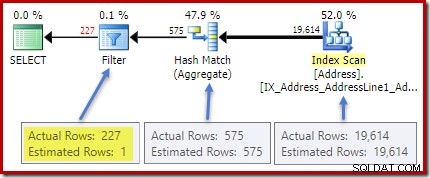
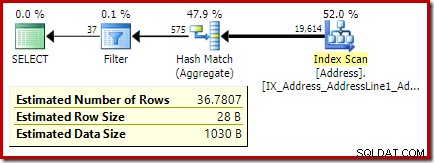
Der (tatsächliche) Nachausführungsplan zeigt eine perfekte Schätzung für das Aggregat; jedoch die Schätzung für das HAVING Klauselfilter (oder Äquivalent in den anderen Abfrageformen) ist schlecht:
Statistiken zur City Spalte liefern genaue Informationen über die Anzahl unterschiedlicher Stadtwerte:
DBCC SHOW_STATISTICS ([Person.Address], City) WITH DENSITY_VECTOR;
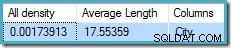
Die alle Dichte Zahl ist der Kehrwert der Anzahl eindeutiger Werte. Einfache Berechnung (1 / 0,00173913) =575 gibt die Kardinalitätsschätzung für das Aggregat an. Die Gruppierung nach Stadt erzeugt offensichtlich eine Zeile für jeden unterschiedlichen Wert.
Beachten Sie, dass alle Dichte kommt vom Dichtevektor. Achten Sie darauf, nicht versehentlich die Dichte zu verwenden Wert aus der Statistikkopfzeilenausgabe von DBCC SHOW_STATISTICS . Die Header-Dichte wird nur aus Gründen der Abwärtskompatibilität beibehalten; es wird heutzutage nicht mehr vom Optimierer während der Kardinalitätsschätzung verwendet.
Das Problem
Das Aggregat führt eine neue berechnete Spalte mit der Bezeichnung Expr1001 in den Arbeitsablauf ein im Ausführungsplan. Es enthält den Wert von COUNT(*) in jeder gruppierten Ausgabezeile:
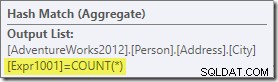
Offensichtlich gibt es in der Datenbank keine statistischen Informationen zu dieser neu berechneten Spalte. Während der Optimierer weiß, dass es 575 Zeilen geben wird, weiß er nichts über die Verteilung von Zählwerten innerhalb dieser Zeilen.
Na ja, nicht ganz nichts:Der Optimierer ist sich bewusst, dass die Zählwerte positive Ganzzahlen (1, 2, 3 …) sein werden. Dennoch ist es die Verteilung dieser ganzzahligen Zählwerte auf die 575 Zeilen, die benötigt würden, um die Selektivität von COUNT(*) = 1 genau abzuschätzen Prädikat.
Man könnte meinen, dass aus dem Histogramm eine Art von Verteilungsinformationen abgeleitet werden könnte, aber das Histogramm liefert nur spezifische Zählinformationen (in EQ_ROWS ) für Histogrammschrittwerte. Zwischen den Histogrammschritten haben wir nur eine Zusammenfassung:RANGE_ROWS Zeilen haben DISTINCT_RANGE_ROWS unterschiedliche Werte. Bei Tabellen, die groß genug sind, dass uns die Qualität der Selektivitätsschätzung wichtig ist, ist es sehr wahrscheinlich, dass der größte Teil der Tabelle durch diese Intra-Step-Zusammenfassungen dargestellt wird.
Zum Beispiel die ersten beiden Zeilen von City Spaltenhistogramm sind:
DBCC SHOW_STATISTICS ([Person.Address], City) WITH HISTOGRAM;

Dies sagt uns, dass es genau eine Zeile für „Abingdon“ und 29 weitere Zeilen nach „Abingdon“, aber vor „Ballard“ gibt, mit 19 unterschiedlichen Werten in diesem 29-Zeilen-Bereich. Die folgende Abfrage zeigt die tatsächliche Verteilung von Zeilen auf eindeutige Werte in diesem 29-Zeilen-Intra-Step-Bereich:
SELECT A.City, NumRows = COUNT_BIG(*) FROM Person.[Address] AS A WHERE A.City > N'Abingdon' AND A.City < N'Ballard' GROUP BY ROLLUP (A.City);

Es gibt 29 Zeilen mit 19 unterschiedlichen Werten, genau wie das Histogramm sagt. Dennoch ist klar, dass wir keine Grundlage haben, um die Selektivität eines Prädikats für die Zählspalte in dieser Abfrage zu bewerten. Beispiel:HAVING COUNT_BIG(*) = 2 würde 5 Zeilen zurückgeben (für Alexandria, Altadena, Atlanta, Augsburg und Austin), aber wir haben keine Möglichkeit, dies anhand des Histogramms zu bestimmen.
Eine fundierte Vermutung
Der Ansatz von SQL Server besteht darin, anzunehmen, dass jede Gruppe am wahrscheinlichsten ist um die gesamte mittlere (durchschnittliche) Anzahl von Zeilen zu enthalten. Dies ist einfach die Kardinalität dividiert durch die Anzahl der eindeutigen Werte. Beispielsweise würde SQL Server für 1000 Zeilen mit 20 eindeutigen Werten davon ausgehen, dass (1000 / 20) =50 Zeilen pro Gruppe der wahrscheinlichste Wert ist.
Zurück zu unserem ursprünglichen Beispiel bedeutet dies, dass die Spalte „berechnete Anzahl“ „höchstwahrscheinlich“ einen Wert um (19614/575) ~=34,1113 enthält . Seit Dichte der Kehrwert der Anzahl eindeutiger Werte ist, können wir auch als Kardinalität * Dichte ausdrücken =(19614 * 0,00173913), was zu einem sehr ähnlichen Ergebnis führt.
Verteilung
Zu sagen, dass der Mittelwert höchstwahrscheinlich ist, führt uns nur so weit. Wir müssen auch genau feststellen, wie wahrscheinlich das ist; und wie sich die Wahrscheinlichkeit ändert, wenn wir uns vom Mittelwert entfernen. Anzunehmen, dass alle Gruppen in unserem Beispiel genau 34.113 Zeilen haben, wäre keine sehr "gebildete" Schätzung!
SQL Server handhabt dies, indem eine Normalverteilung angenommen wird. Diese hat die charakteristische Glockenform, die Sie vielleicht schon kennen (Bild aus dem verlinkten Wikipedia-Eintrag):
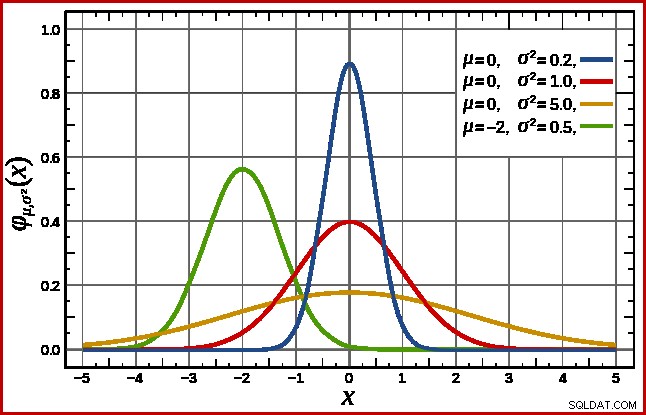
Die genaue Form der Normalverteilung hängt von zwei Parametern ab :der Mittelwert (µ ) und die Standardabweichung (σ ). Der Mittelwert bestimmt die Lage des Peaks. Die Standardabweichung gibt an, wie „abgeflacht“ die Glockenkurve ist. Je flacher die Kurve, desto niedriger ist der Peak und desto mehr verteilt sich die Wahrscheinlichkeitsdichte auf andere Werte.
Wie bereits erwähnt, kann SQL Server den Mittelwert aus statistischen Informationen ableiten. Die Standardabweichung der berechneten Zählspaltenwerte ist unbekannt. SQL Server schätzt es als Quadratwurzel des Mittelwerts (mit einer geringfügigen Anpassung, die später beschrieben wird). In unserem Beispiel bedeutet dies, dass die beiden Parameter der Normalverteilung ungefähr 34,1113 und 5,84 (die Quadratwurzel) betragen.
Der Standard Die Normalverteilung (die rote Kurve im obigen Diagramm) ist ein bemerkenswerter Sonderfall. Dies tritt auf, wenn der Mittelwert Null und die Standardabweichung 1 ist. Jede Normalverteilung kann in die Standardnormalverteilung umgewandelt werden, indem der Mittelwert subtrahiert und durch die Standardabweichung geteilt wird.
Bereiche und Intervalle
Wir sind daran interessiert, die Selektivität zu schätzen, also suchen wir nach der Wahrscheinlichkeit, dass die berechnete Anzahl-Spalte einen bestimmten Wert (x) hat. Diese Wahrscheinlichkeit ergibt sich nicht aus dem Wert auf der y-Achse oben, sondern aus der Fläche unter der Kurve links von x.
Für die Normalverteilung mit Mittelwert 34,1113 und Standardabweichung 5,84 beträgt die Fläche unter der Kurve links von x =30 etwa 0,2406:
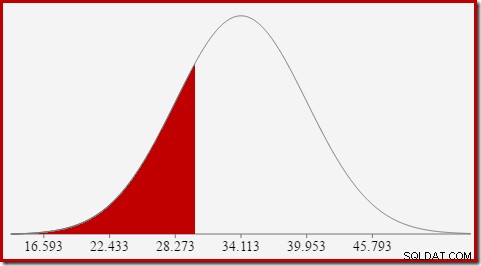
Dies entspricht der Wahrscheinlichkeit, dass die berechnete Anzahlspalte kleiner oder gleich ist 30 für unsere Beispielabfrage.
Dies führt zu der Idee, dass wir im Allgemeinen nicht nach der Wahrscheinlichkeit eines bestimmten Werts suchen, sondern nach einem Intervall . Um die wahrscheinlich zu finden, dass die Anzahl gleich ist ein ganzzahliger Wert, müssen wir die Tatsache berücksichtigen, dass ganze Zahlen ein Intervall der Größe 1 überspannen. Wie wir eine ganze Zahl in ein Intervall umwandeln, ist etwas willkürlich. SQL Server verarbeitet dies durch Addieren und Subtrahieren von 0,5 um die untere und obere Grenze des Intervalls anzugeben.
Um beispielsweise die Wahrscheinlichkeit zu finden, dass der berechnete Zählwert gleich 30 ist, müssen wir subtrahieren die Fläche unter der Normalverteilungskurve für (x =29,5) von der Fläche für (x =30,5). Das Ergebnis entspricht dem Slice für (29,5
Die Fläche der roten Scheibe beträgt etwa 0,0533 . In einer guten ersten Annäherung ist dies die Selektivität eines Prädikats count =30 in unserer Testabfrage.
Die Berechnung der Fläche unter einer Normalverteilung links von einem bestimmten Wert ist nicht einfach. Die allgemeine Formel ist durch die kumulative Verteilungsfunktion (CDF) gegeben. Das Problem ist, dass die CDF nicht in Form von elementaren mathematischen Funktionen ausgedrückt werden kann, sodass stattdessen numerische Näherungsverfahren verwendet werden müssen.
Da alle Normalverteilungen leicht in die Standardnormalverteilung transformiert werden können (Mittelwert =0, Standardabweichung =1), funktionieren alle Annäherungen, um die Standardnormale zu schätzen. Das bedeutet, dass wir uns transformieren müssen unsere Intervallgrenzen von der speziellen Normalverteilung, die für die Abfrage geeignet ist, zur Standardnormalverteilung. Dazu wird, wie bereits erwähnt, der Mittelwert subtrahiert und durch die Standardabweichung dividiert.
Wenn Sie mit Excel vertraut sind, sind Ihnen vielleicht die Funktionen NORM.DIST und NORM.S.DIST bekannt, die CDFs (unter Verwendung numerischer Näherungsmethoden) für eine bestimmte Normalverteilung oder die Standardnormalverteilung berechnen können.
In SQL Server ist kein CDF-Rechner integriert, aber wir können ganz einfach einen erstellen. Vorausgesetzt, dass die CDF für die Standardnormalverteilung ist:
…wo erf ist die Fehlerfunktion:
Eine T-SQL-Implementierung zum Abrufen der CDF für die Standardnormalverteilung ist unten dargestellt. Es verwendet eine numerische Annäherung für die Fehlerfunktion das kommt dem sehr nahe, das SQL Server intern verwendet:
Ein Beispiel, um die CDF für x =30 unter Verwendung der Normalverteilung für unsere Testabfrage zu berechnen:
Beachten Sie den Normalisierungsschritt zum Konvertieren in die Standardnormalverteilung. Die Prozedur gibt den Wert 0,2407196… zurück, der mit sieben Nachkommastellen dem entsprechenden Excel-Ergebnis entspricht.
Der folgende Code ändert unsere Beispielabfrage, um eine größere Schätzung für den Filter zu erzeugen (der Vergleich erfolgt jetzt mit dem Wert 32, der viel näher am Mittelwert liegt als zuvor):
Die Schätzung des Optimierungsprogramms beträgt jetzt 36,7807 .
Um die Schätzung manuell zu berechnen, müssen wir uns zunächst mit einigen abschließenden Details befassen:
Das folgende Verfahren enthält alle Details in diesem Artikel. Es erfordert die zuvor angegebene CDF-Prozedur:
Wir können jetzt dieses Verfahren verwenden, um eine Schätzung für unsere neue Testabfrage zu generieren:
Die Ausgabe ist:
Dies lässt sich sehr gut mit der Kardinalitätsschätzung des Optimierers von 36,7807. vergleichen
Das Verfahren kann für andere Zählintervalle als Gleichheitsprüfungen verwendet werden. Es muss lediglich der
Um dies mit unserer Prozedur zu verwenden, setzen wir
Das Ergebnis ist 572.5964:
Ein letztes Beispiel mit
Die Optimierungsschätzung ist
Seit
Auch dies stimmt mit der Optimierungsschätzung überein.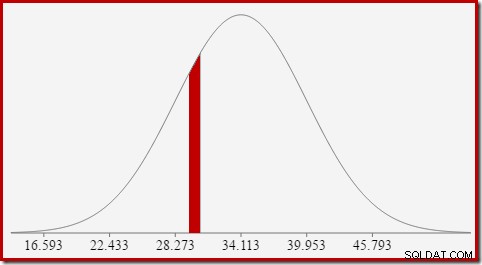
Die kumulative Verteilungsfunktion
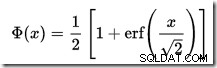
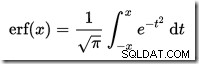
CREATE PROCEDURE dbo.GetStandardNormalCDF
(
@x float,
@cdf float OUTPUT
)
AS
BEGIN
SET NOCOUNT, XACT_ABORT ON;
DECLARE
@sign float,
@erf float;
SET @sign = SIGN(@x);
SET @x = ABS(@x) / SQRT(2);
SET @erf = 1;
SET @erf = @erf + (0.0705230784 * @x);
SET @erf = @erf + (0.0422820123 * POWER(@x, 2));
SET @erf = @erf + (0.0092705272 * POWER(@x, 3));
SET @erf = @erf + (0.0001520143 * POWER(@x, 4));
SET @erf = @erf + (0.0002765672 * POWER(@x, 5));
SET @erf = @erf + (0.0000430638 * POWER(@x, 6));
SET @erf = POWER(@erf, -16);
SET @erf = 1 - @erf;
SET @erf = @erf * @sign;
SET @cdf = 0.5 * (1 + @erf);
END; DECLARE @cdf float;
DECLARE @x float;
-- HAVING COUNT_BIG(*) = x
SET @x = 30;
-- Normalize 30 by subtracting the mean
-- and dividing by the standard deviation
SET @x = (@x - 34.1113) / 5.84;
EXECUTE dbo.GetStandardNormalCDF
@x = @x,
@cdf = @cdf OUTPUT;
SELECT CDF = @cdf; Letzte Details und Beispiele
SELECT A.City
FROM Person.[Address] AS A
GROUP BY A.City
HAVING COUNT_BIG(*) = 32;
COUNT(*) = 1 , die hier nicht näher ausgeführt wird. COUNT(*) = 1 In diesem Fall verwendet das Legacy-CE dieselbe Logik wie das neue CE (verfügbar ab SQL Server 2014).CREATE PROCEDURE dbo.GetCountPredicateEstimate
(
@From integer,
@To integer,
@Cardinality float,
@Density float,
@Selectivity float OUTPUT,
@Estimate float OUTPUT
)
AS
BEGIN
SET NOCOUNT, XACT_ABORT ON;
BEGIN TRY
DECLARE
@Start float,
@End float,
@Distinct float,
@Mean float,
@MeanAdj float,
@Stdev float,
@NormStart float,
@NormEnd float,
@CDFStart float,
@CDFEnd float;
-- Validate input and apply defaults
IF ISNULL(@From, 0) = 0 SET @From = 1;
IF @From < 1 RAISERROR ('@From must be >= 1', 16, 1);
IF ISNULL(@Cardinality, -1) <= 0 RAISERROR('@Cardinality must be positive', 16, 1);
IF ISNULL(@Density, -1) <= 0 RAISERROR('@Density must be positive', 16, 1);
IF ISNULL(@To, 0) = 0 SET @To = CEILING(1 / @Density);
IF @To < @From RAISERROR('@To must be >= @From', 16, 1);
-- Convert integer range to interval
SET @Start = @From - 0.5;
SET @End = @To + 0.5;
-- Get number of distinct values
SET @Distinct = 1 / @Density;
-- Calculate mean
SET @Mean = @Cardinality * @Density;
-- Adjust mean;
SET @MeanAdj = @Mean * ((@Distinct - 1) / @Distinct);
-- Get standard deviation (guess)
SET @Stdev = SQRT(@MeanAdj);
-- Normalize interval
SET @NormStart = (@Start - @Mean) / @Stdev;
SET @NormEnd = (@End - @Mean) / @Stdev;
-- Calculate CDFs
EXECUTE dbo.GetStandardNormalCDF
@x = @NormStart,
@cdf = @CDFStart OUTPUT;
EXECUTE dbo.GetStandardNormalCDF
@x = @NormEnd,
@cdf = @CDFEnd OUTPUT;
-- Selectivity
SET @Selectivity =
CASE
-- Unbounded start
WHEN @From = 1 THEN @CDFEnd
-- Unbounded end
WHEN @To >= @Distinct THEN 1 - @CDFStart
-- Normal interval
ELSE @CDFEnd - @CDFStart
END;
-- Return row estimate
SET @Estimate = @Selectivity * @Distinct;
END TRY
BEGIN CATCH
DECLARE @EM nvarchar(4000) = ERROR_MESSAGE();
IF @@TRANCOUNT > 0 ROLLBACK TRANSACTION;
RAISERROR (@EM, 16, 1);
RETURN;
END CATCH;
END; DECLARE
@Selectivity float,
@Estimate float;
EXECUTE dbo.GetCountPredicateEstimate
@From = 32,
@To = 32,
@Cardinality = 19614,
@Density = 0.00173913,
@Selectivity = @Selectivity OUTPUT,
@Estimate = @Estimate OUTPUT;
SELECT
Selectivity = @Selectivity,
Estimate = @Estimate,
Rounded = ROUND(@Estimate, 4); 
Beispiele für Ungleichheitsintervalle
@From gesetzt werden und @To Parameter zu den ganzzahligen Intervallgrenzen. Um unbegrenzt anzugeben, übergeben Sie Null oder NULL wie Sie es bevorzugen.SELECT A.City
FROM Person.[Address] AS A
GROUP BY A.City
HAVING COUNT_BIG(*) < 50;

@From = NULL und @To = 49 (weil 50 von weniger als ausgeschlossen wird):DECLARE
@Selectivity float,
@Estimate float;
EXECUTE dbo.GetCountPredicateEstimate
@From = NULL,
@To = 49,
@Cardinality = 19614,
@Density = 0.00173913,
@Selectivity = @Selectivity OUTPUT,
@Estimate = @Estimate OUTPUT;
SELECT
Selectivity = @Selectivity,
Estimate = @Estimate,
Rounded = ROUND(@Estimate, 4); 
BETWEEN :SELECT A.City
FROM Person.[Address] AS A
GROUP BY A.City
HAVING COUNT_BIG(*) BETWEEN 25 AND 30;

BETWEEN inklusive ist, übergeben wir die Prozedur @From = 25 und @To = 30 . Das Ergebnis ist: