Letzten Monat habe ich Peter Larssons Rätsel behandelt, wie Angebot und Nachfrage aufeinander abgestimmt werden können. Ich habe Peters einfache Cursor-basierte Lösung gezeigt und erklärt, dass sie eine lineare Skalierung hat. Die Herausforderung, die ich Ihnen hinterlassen habe, besteht darin, zu versuchen, eine satzbasierte Lösung für die Aufgabe zu finden, und Junge, lassen Sie die Leute sich der Herausforderung stellen! Danke Luca, Kamil Kosno, Daniel Brown, Brian Walker, Joe Obbish, Rainer Hoffmann, Paul White, Charlie und natürlich Peter Larsson für die Zusendung Ihrer Lösungen. Einige der Ideen waren brillant und geradezu überwältigend.
Diesen Monat werde ich damit beginnen, die eingereichten Lösungen grob zu untersuchen, und zwar von den schlechteren zu den leistungsstärksten. Warum sollte man sich überhaupt mit den schlecht performenden beschäftigen? Weil man noch viel von ihnen lernen kann; zum Beispiel durch Identifizieren von Antimustern. In der Tat basiert der erste Versuch, diese Herausforderung für viele Menschen, einschließlich mir und Peter, zu lösen, auf einem Intervallschnittkonzept. Es kommt vor, dass die klassische Prädikat-basierte Technik zum Identifizieren von Intervallüberschneidungen eine schlechte Leistung aufweist, da es kein gutes Indizierungsschema gibt, um sie zu unterstützen. Dieser Artikel ist diesem leistungsschwachen Ansatz gewidmet. Trotz der schlechten Performance ist die Arbeit an der Lösung eine interessante Übung. Es erfordert das Üben der Fähigkeit, das Problem so zu modellieren, dass es sich für eine satzbasierte Behandlung eignet. Es ist auch interessant, den Grund für die schlechte Leistung zu identifizieren, wodurch es einfacher wird, das Anti-Pattern in Zukunft zu vermeiden. Denken Sie daran, dass diese Lösung nur der Anfang ist.
DDL und ein kleiner Satz von Beispieldaten
Zur Erinnerung:Die Aufgabe umfasst das Abfragen einer Tabelle mit dem Namen "Auktionen". Verwenden Sie den folgenden Code, um die Tabelle zu erstellen und sie mit einem kleinen Satz von Beispieldaten zu füllen:
DROPT TABLE IF EXISTS dbo.Auctions; CREATE TABLE dbo.Auctions( ID INT NOT NULL IDENTITY(1, 1) CONSTRAINT pk_Auctions PRIMARY KEY CLUSTERED, Code CHAR(1) NOT NULL CONSTRAINT ck_Auctions_Code CHECK (Code ='D' OR Code ='S'), Quantity DECIMAL(19 , 6) NOT NULL CONSTRAINT ck_Auctions_Quantity CHECK (Menge> 0)); NOCOUNT EINSTELLEN; AUS dbo.Auctions LÖSCHEN; SET IDENTITY_INSERT dbo.Auctions ON; INSERT INTO dbo.Auctions(ID, Code, Menge) WERTE (1, 'D', 5.0), (2, 'D', 3.0), (3, 'D', 8.0), (5, 'D', 2.0), (6, 'D', 8.0), (7, 'D', 4.0), (8, 'D', 2.0), (1000, 'S', 8.0), (2000, 'S', 6.0), (3000, 'S', 2.0), (4000, 'S', 2.0), (5000, 'S', 4.0), (6000, 'S', 3.0), (7000, 'S', 2,0); SET IDENTITY_INSERT dbo.Auctions OFF;
Ihre Aufgabe bestand darin, Paarungen zu erstellen, die Angebots- und Bedarfseinträge basierend auf der ID-Reihenfolge abgleichen, und diese in eine temporäre Tabelle zu schreiben. Nachfolgend das gewünschte Ergebnis für den kleinen Satz von Beispieldaten:
DemandID SupplyID TradeQuantity----------- ----------- --------------1 1000 5.0000002 1000 3.0000003 2000 6.0000003 3000 2,0000005 4000 2,0000006 5000 4,0000006 6000 3,0000006 7000 1,0000007 7000 1,000000
Letzten Monat habe ich auch Code bereitgestellt, den Sie verwenden können, um die Auktionstabelle mit einem großen Satz von Beispieldaten zu füllen und die Anzahl der Angebots- und Nachfrageeinträge sowie deren Mengenbereich zu steuern. Stellen Sie sicher, dass Sie den Code aus dem Artikel des letzten Monats verwenden, um die Leistung der Lösungen zu überprüfen.
Modellierung der Daten als Intervalle
Eine faszinierende Idee, die sich zur Unterstützung satzbasierter Lösungen eignet, besteht darin, die Daten als Intervalle zu modellieren. Mit anderen Worten, stellen Sie jeden Bedarfs- und Angebotseintrag als Intervall dar, beginnend mit der laufenden Summe gleichartiger Mengen (Bedarf oder Angebot) bis zum, aber ohne Strom, und endend mit der laufenden Summe einschließlich des Stroms, natürlich basierend auf der ID Bestellung. Wenn Sie sich beispielsweise den kleinen Satz von Beispieldaten ansehen, ist der erste Bedarfseintrag (ID 1) für eine Menge von 5,0 und der zweite (ID 2) für eine Menge von 3,0. Der erste Bedarfseintrag kann mit dem Intervallbeginn:0,0, Ende:5,0 und der zweite mit dem Intervallbeginn:5,0, Ende:8,0 usw. dargestellt werden.
In ähnlicher Weise kann der erste Angebotseintrag (ID 1000) dargestellt werden. steht für eine Menge von 8,0 und die zweite (ID 2000) für eine Menge von 6,0. Der erste Angebotseintrag kann mit dem Intervallstart:0,0, Ende:8,0 und der zweite mit dem Intervallstart:8,0, Ende:14,0 usw. dargestellt werden.
Die Bedarfs-Angebots-Paarungen, die Sie erstellen müssen, sind dann die überlappenden Segmente der sich überschneidenden Intervalle zwischen den beiden Arten.
Dies lässt sich wahrscheinlich am besten anhand einer visuellen Darstellung der intervallbasierten Modellierung der Daten und des gewünschten Ergebnisses verstehen, wie in Abbildung 1 gezeigt.
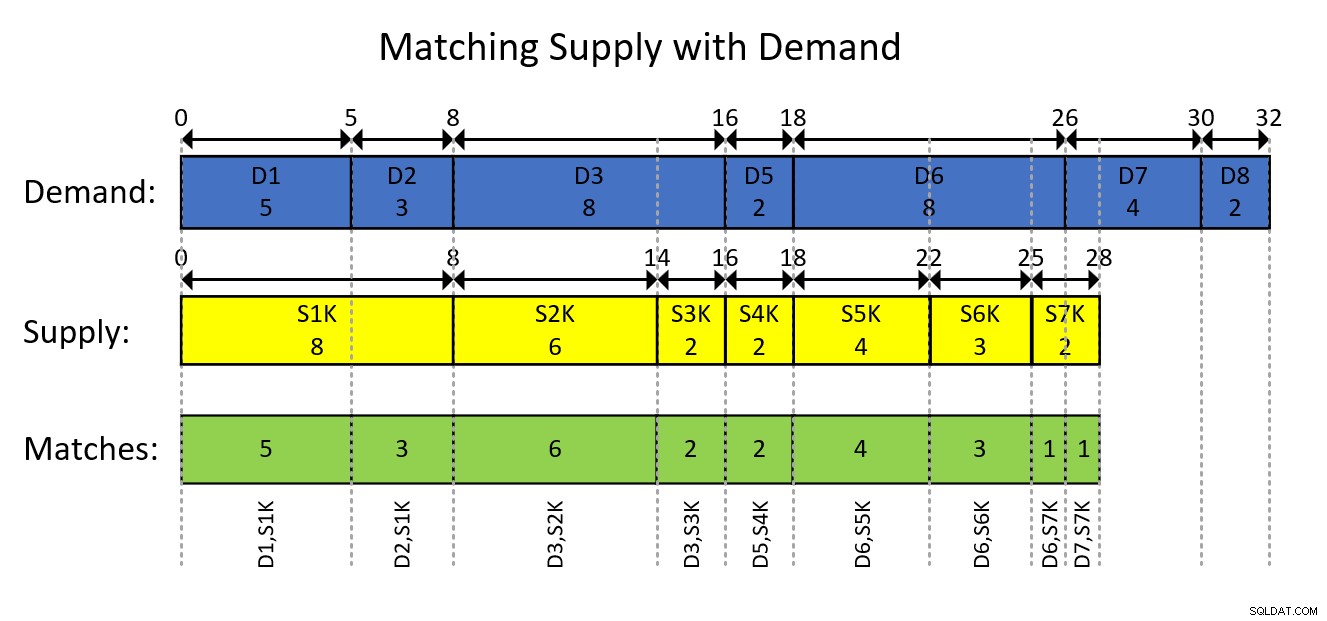Abbildung 1:Modellierung der Daten als Intervalle
Die visuelle Darstellung in Abbildung 1 ist ziemlich selbsterklärend, aber kurz gesagt …
Die blauen Rechtecke stellen die Bedarfseinträge als Intervalle dar, wobei die exklusive laufende Summenmengen als Beginn des Intervalls und die inklusiven laufenden Summen als Ende des Intervalls angezeigt werden. Die gelben Rechtecke tun dasselbe für Versorgungseinträge. Beachten Sie dann, wie die überlappenden Segmente der sich überschneidenden Intervalle der beiden Arten, die durch die grünen Rechtecke dargestellt sind, die Nachfrage-Angebots-Paare sind, die Sie erzeugen müssen. Die erste Ergebnispaarung ist beispielsweise mit Bedarfs-ID 1, Angebots-ID 1000, Menge 5. Die zweite Ergebnispaarung ist mit Bedarfs-ID 2, Angebots-ID 1000, Menge 3. Und so weiter.
Intervallschnitte mit CTEs
Bevor Sie beginnen, den T-SQL-Code mit Lösungen zu schreiben, die auf der Idee der Intervallmodellierung basieren, sollten Sie bereits ein intuitives Gespür dafür haben, welche Indizes hier wahrscheinlich nützlich sind. Da Sie wahrscheinlich Fensterfunktionen verwenden, um laufende Summen zu berechnen, könnten Sie von einem abdeckenden Index mit einem Schlüssel profitieren, der auf den Spalten Code, ID und einschließlich der Spalte Menge basiert. Hier ist der Code, um einen solchen Index zu erstellen:
EINZIGARTIGEN, NICHT EINGESCHLOSSENEN INDEX ERSTELLEN idx_Code_ID_i_Quantity ON dbo.Auctions(Code, ID) INCLUDE(Quantity);
Das ist derselbe Index, den ich für die Cursor-basierte Lösung empfohlen habe, die ich letzten Monat behandelt habe.
Außerdem besteht hier Potenzial, um von der Stapelverarbeitung zu profitieren. Sie können seine Berücksichtigung ohne die Anforderungen des Stapelmodus im Rowstore aktivieren, z. B. mit SQL Server 2019 Enterprise oder höher, indem Sie den folgenden Dummy-Columnstore-Index erstellen:
CREATE NONCLUSTERED COLUMNSTORE INDEX idx_cs ON dbo.Auctions(ID) WHERE ID =-1 AND ID =-2;
Sie können jetzt mit der Arbeit am T-SQL-Code der Lösung beginnen.
Der folgende Code erstellt die Intervalle, die die Bedarfseinträge darstellen:
WITH D0 AS-- D0 berechnet die laufende Nachfrage als EndDemand( SELECT ID, Quantity, SUM(Menge) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand FROM dbo.Auctions WHERE Code ='D'),-- D extrahiert prev EndDemand als StartDemand, wobei der Start-End-Bedarf als ein Intervall D AS( SELECT ID, Quantity, EndDemand - Quantity AS StartDemand, EndDemand FROM D0)SELECT *FROM D;ausgedrückt wird
Die Abfrage, die den CTE D0 definiert, filtert Bedarfseinträge aus der Auktionstabelle und berechnet eine laufende Gesamtmenge als Endbegrenzer der Bedarfsintervalle. Dann fragt die Abfrage, die den zweiten CTE namens D definiert, D0 ab und berechnet den Startbegrenzer der Bedarfsintervalle durch Subtrahieren der aktuellen Menge vom Endbegrenzer.
Dieser Code generiert die folgende Ausgabe:
ID Menge StartDemand EndDemand---- --------- ------------ ----------1 5.000000 0.000000 5.0000002 3.000000 5.000000 8.0000003 8.000000 8.000000 16.0000005 2.000000 16.000000 18.0000006 8.000000 18.000000 26.0000007 4.000000 26.000000 30.0000008 2.000000 30.000 30.000Die Lieferintervalle werden sehr ähnlich generiert, indem die gleiche Logik auf die Liefereinträge angewendet wird, indem der folgende Code verwendet wird:
WITH S0 AS-- S0 berechnet das laufende Angebot als EndSupply( SELECT ID, Quantity, SUM(Quantity) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndSupply FROM dbo.Auctions WHERE Code ='S'),-- S extrahiert prev EndSupply als StartSupply, wobei Start-End-Versorgung als Intervall ausgedrückt wird AS( SELECT ID, Quantity, EndSupply - Quantity AS StartSupply, EndSupply FROM S0)SELECT *FROM S;Dieser Code generiert die folgende Ausgabe:
ID Menge StartSupply EndSupply----- --------- ------------ ----------1000 8.000000 0.000000 8.0000002000 6.000000 8.000000 14.0000003000 2.000000 14.000000 16.0000004000 2.000000 16.000000 18.0000005000 4.000000 18.000000 22.0000006000 3.000000 22.000000 25.0000007000 2.000000 25.000000 27.00000000Was übrig bleibt, ist dann, die sich schneidenden Nachfrage- und Angebotsintervalle aus den CTEs D und S zu identifizieren und die überlappenden Segmente dieser sich schneidenden Intervalle zu berechnen. Denken Sie daran, dass die Ergebnispaarungen in eine temporäre Tabelle geschrieben werden sollten. Dies kann mit dem folgenden Code erfolgen:
-- Temporäre Tabelle löschen, falls vorhanden DROP TABLE IF EXISTS #MyPairings; WITH D0 AS-- D0 berechnet den laufenden Bedarf als EndDemand( SELECT ID, Quantity, SUM(Menge) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand FROM dbo.Auctions WHERE Code ='D'),-- D extrahiert den vorherigen EndDemand als StartDemand, wobei der Start-End-Bedarf als ein Intervall ausgedrückt wird D AS( SELECT ID, Quantity, EndDemand - Quantity AS StartDemand, EndDemand FROM D0),S0 AS-- S0 berechnet den laufenden Vorrat als EndSupply( SELECT ID, Quantity, SUM(Quantity) OVER (ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndSupply FROM dbo.Auctions WHERE Code ='S'),-- S extrahiert das vorherige EndSupply als StartSupply und drückt das Start-End-Angebot als Intervall AS aus (SELECT ID, Quantity, EndSupply - Quantity AS StartSupply, EndSupply FROM S0) – Äußere Abfrage identifiziert Trades als die überlappenden Segmente der sich überschneidenden Intervalle – In den sich überschneidenden Nachfrage- und Angebotsintervallen ist die Handelsmenge dann – LEAST(EndDemand, EndSupply) – GRÖSSTE(StartDemsnad, StartSupply)SELECT D.ID AS DemandID, S.ID AS SupplyID, CASE WH EN EndDemandStartSupply THEN StartDemand ELSE StartSupply END AS TradeQuantityINTO #MyPairingsFROM D INNER JOIN S ON D.StartDemand S.StartSupply; Neben dem Code, der die Bedarfs- und Angebotsintervalle erstellt, den Sie bereits früher gesehen haben, ist die wichtigste Ergänzung hier die äußere Abfrage, die die sich überschneidenden Intervalle zwischen D und S identifiziert und die überlappenden Segmente berechnet. Um die sich überschneidenden Intervalle zu identifizieren, verbindet die äußere Abfrage D und S mit dem folgenden Join-Prädikat:
D.StartDemandS.StartSupply Das ist das klassische Prädikat, um Intervallschnittpunkte zu identifizieren. Es ist auch die Hauptursache für die schlechte Leistung der Lösung, wie ich gleich erklären werde.
Die äußere Abfrage berechnet auch die Handelsmenge in der SELECT-Liste wie folgt:
LEAST(EndDemand, EndSupply) - GRÖSSTE(StartDemand, StartSupply)Wenn Sie Azure SQL verwenden, können Sie diesen Ausdruck verwenden. Wenn Sie SQL Server 2019 oder früher verwenden, können Sie die folgende logisch äquivalente Alternative verwenden:
CASE WHEN EndDemandStartSupply THEN StartDemand ELSE StartSupply END Da das Ergebnis in eine temporäre Tabelle geschrieben werden sollte, verwendet die äußere Abfrage eine SELECT INTO-Anweisung, um dies zu erreichen.
Die Idee, die Daten als Intervalle zu modellieren, ist eindeutig faszinierend und elegant. Aber was ist mit der Leistung? Leider hat diese spezifische Lösung ein großes Problem in Bezug darauf, wie Intervallüberschneidungen identifiziert werden. Untersuchen Sie den in Abbildung 2 gezeigten Plan für diese Lösung.
Abbildung 2:Abfrageplan für Kreuzungen mit CTEs-Lösung
Beginnen wir mit den kostengünstigen Teilen des Plans.
Die äußere Eingabe des Nested-Loops-Joins berechnet die Bedarfsintervalle. Es verwendet einen Indexsuchoperator, um die Bedarfseinträge abzurufen, und einen Window-Aggregate-Operator im Stapelmodus, um das Begrenzungszeichen für das Ende des Bedarfsintervalls zu berechnen (in diesem Plan als „Expr1005“ bezeichnet). Das Anfangstrennzeichen für das Bedarfsintervall ist dann Expr1005 – Menge (von D).
Als Nebenbemerkung könnte Sie die Verwendung eines expliziten Sort-Operators vor dem Window Aggregate-Operator im Stapelmodus hier überraschen, da die aus Index Seek abgerufenen Bedarfseinträge bereits nach ID sortiert sind, wie es die Fensterfunktion benötigt. Dies hat mit der Tatsache zu tun, dass SQL Server derzeit keine effiziente Kombination aus einer parallelen, die Reihenfolge beibehaltenden Indexoperation vor einem parallelen Batchmodus-Window-Aggregate-Operator unterstützt. Wenn Sie einen seriellen Plan nur zu Experimentierzwecken erzwingen, wird der Sort-Operator verschwinden. SQL Server hat insgesamt entschieden, dass hier die Verwendung von Parallelität bevorzugt wird, obwohl dies zu der hinzugefügten expliziten Sortierung führt. Aber noch einmal, dieser Teil des Plans stellt einen kleinen Teil der Arbeit im großen Ganzen dar.
In ähnlicher Weise beginnt die innere Eingabe des Joins mit verschachtelten Schleifen mit der Berechnung der Versorgungsintervalle. Seltsamerweise entschied sich SQL Server für die Verwendung von Operatoren im Zeilenmodus, um diesen Teil zu handhaben. Einerseits verursachen Operatoren im Zeilenmodus, die zum Berechnen laufender Summen verwendet werden, mehr Overhead als die Window Aggregate-Alternative im Stapelmodus. Auf der anderen Seite verfügt SQL Server über eine effiziente parallele Implementierung einer reihenfolgeerhaltenden Indexoperation, die auf die Berechnung der Fensterfunktion folgt, wodurch eine explizite Sortierung für diesen Teil vermieden wird. Es ist merkwürdig, dass der Optimierer eine Strategie für die Bedarfsintervalle und eine andere für die Versorgungsintervalle gewählt hat. Auf jeden Fall ruft der Indexsuchoperator die Versorgungseinträge ab, und die nachfolgende Folge von Operatoren bis zum Compute Scalar-Operator berechnet den Versorgungsintervall-Endbegrenzer (in diesem Plan als Expr1009 bezeichnet). Das Anfangstrennzeichen für das Lieferintervall ist dann Expr1009 – Menge (von S).
Trotz der Menge an Text, die ich verwendet habe, um diese beiden Teile zu beschreiben, kommt der wirklich kostspielige Teil der Arbeit im Plan als nächstes.
Der nächste Teil muss die Bedarfsintervalle und die Angebotsintervalle mit dem folgenden Prädikat verbinden:
D.StartDemandS.StartSupply Ohne unterstützenden Index würde dies unter der Annahme von DI-Nachfrageintervallen und SI-Versorgungsintervallen die Verarbeitung von DI * SI-Zeilen beinhalten. Der Plan in Abbildung 2 wurde erstellt, nachdem die Auktionstabelle mit 400.000 Zeilen gefüllt wurde (200.000 Nachfrageeinträge und 200.000 Angebotseinträge). Ohne unterstützenden Index hätte der Plan also 200.000 * 200.000 =40.000.000.000 Zeilen verarbeiten müssen. Um diese Kosten zu mindern, entschied sich der Optimierer, einen temporären Index (siehe Index-Spool-Operator) mit dem Begrenzer für das Ende des Lieferintervalls (Expr1009) als Schlüssel zu erstellen. Das ist so ziemlich das Beste, was es tun konnte. Dies löst jedoch nur einen Teil des Problems. Bei zwei Bereichsprädikaten kann nur eines von einem Indexsuchprädikat unterstützt werden. Der andere muss mit einem Restprädikat behandelt werden. Tatsächlich können Sie im Plan sehen, dass die Suche im temporären Index das Suchprädikat Expr1009> Expr1005 – D.Quantity verwendet, gefolgt von einem Filteroperator, der das Restprädikat Expr1005> Expr1009 – S.Quantity handhabt.
Unter der Annahme, dass das Suchprädikat im Durchschnitt die Hälfte der Angebotszeilen aus dem Index pro Nachfragezeile isoliert, beträgt die Gesamtzahl der vom Index Spool-Operator ausgegebenen und vom Filter-Operator verarbeiteten Zeilen dann DI * SI / 2. In unserem Fall mit 200.000 Nachfragezeilen und 200.000 Angebotszeilen ergibt dies 20.000.000.000. Tatsächlich zeigt der Pfeil, der vom Index-Spool-Operator zum Filter-Operator geht, eine Reihe von Zeilen in der Nähe davon an.
Dieser Plan hat eine quadratische Skalierung im Vergleich zur linearen Skalierung der Cursor-basierten Lösung vom letzten Monat. Sie können das Ergebnis eines Leistungstests sehen, in dem die beiden Lösungen in Abbildung 3 verglichen werden. Sie können deutlich die schön geformte Parabel für die satzbasierte Lösung erkennen.
Abbildung 3:Leistung von Schnittpunkten mit CTEs-Lösung im Vergleich zu einer Cursor-basierten Lösung
Intervallschnitte mit temporären Tabellen
Sie können die Dinge etwas verbessern, indem Sie die Verwendung von CTEs für die Bedarfs- und Versorgungsintervalle durch temporäre Tabellen ersetzen und zur Vermeidung des Index-Spools Ihren eigenen Index für die temporäre Tabelle erstellen, der die Versorgungsintervalle mit dem Endbegrenzer als Schlüssel enthält. Hier ist der Code der vollständigen Lösung:
-- Temporäre Tabellen löschen, falls vorhanden DROP TABLE IF EXISTS #MyPairings, #Demand, #Supply; WITH D0 AS-- D0 berechnet den laufenden Bedarf als EndDemand( SELECT ID, Quantity, SUM(Menge) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndDemand FROM dbo.Auctions WHERE Code ='D'),-- D extrahiert den vorherigen EndDemand as StartDemand, wobei der Start-End-Bedarf als ein Intervall ausgedrückt wird D AS( SELECT ID, Quantity, EndDemand - Quantity AS StartDemand, EndDemand FROM D0)SELECT ID, Quantity, CAST(ISNULL(StartDemand, 0.0) AS DECIMAL(19, 6)) AS StartDemand, CAST(ISNULL(EndDemand, 0.0) AS DECIMAL(19, 6)) AS EndDemandINTO #DemandFROM D;MIT S0 AS-- S0 berechnet den laufenden Vorrat als EndSupply( SELECT ID, Quantity, SUM(Menge) OVER(ORDER BY ID ROWS UNBOUNDED PRECEDING) AS EndSupply FROM dbo.Auctions WHERE Code ='S'),-- S extrahiert prev EndSupply als StartSupply und drückt Start-End-Angebot als Intervall aus AS( SELECT ID, Quantity, EndSupply - Quantity AS StartSupply, EndSupply FROM S0)SELECT ID, Menge, CAST(ISNULL(StartSupply, 0.0) AS DECIMAL(19, 6)) AS StartSupply, CAST(ISNULL(EndSupply, 0.0) AS DECIMAL(19, 6)) AS EndSupplyINTO #SupplyFROM S; EINZIGARTIGEN CLUSTERED INDEX ERSTELLEN idx_cl_ES_ID ON #Supply(EndSupply, ID); -- Äußere Abfrage identifiziert Trades als die überlappenden Segmente der sich überschneidenden Intervalle-- In den sich überschneidenden Nachfrage- und Angebotsintervallen ist die Handelsmenge dann -- LEAST(EndDemand, EndSupply) - GRÖSSTE(StartDemsnad, StartSupply)SELECT D.ID AS DemandID, S.ID AS SupplyID, CASE WHEN EndDemandStartSupply THEN StartDemand ELSE StartSupply END AS TradeQuantityINTO #MyPairingsFROM #Demand AS D INNER JOIN #Supply AS S WITH (FORCESEEK) ON D.StartDemand S.StartSupply; Die Pläne für diese Lösung sind in Abbildung 4 dargestellt:
Abbildung 4:Abfrageplan für Schnittpunkte mithilfe der temporären Tabellenlösung
Die ersten beiden Pläne verwenden eine Kombination aus Indexsuch-, Sortier- und Fensteraggregationsoperatoren im Stapelmodus, um die Angebots- und Nachfrageintervalle zu berechnen und diese in temporäre Tabellen zu schreiben. Der dritte Plan behandelt die Indexerstellung für die #Supply-Tabelle mit dem EndSupply-Trennzeichen als führendem Schlüssel.
Der vierte Plan stellt bei weitem den Großteil der Arbeit dar, mit einem Nested-Loops-Join-Operator, der mit jedem Intervall von #Demand übereinstimmt, den sich überschneidenden Intervallen von #Supply. Beachten Sie, dass sich der Indexsuchoperator auch hier auf das Prädikat #Supply.EndSupply> #Demand.StartDemand als Suchprädikat und #Demand.EndDemand> #Supply.StartSupply als Restprädikat stützt. In Bezug auf Komplexität/Skalierung erhalten Sie also die gleiche quadratische Komplexität wie für die vorherige Lösung. Sie zahlen nur weniger pro Zeile, da Sie Ihren eigenen Index anstelle der Indexspule des vorherigen Plans verwenden. Sie können die Leistung dieser Lösung im Vergleich zu den beiden vorherigen in Abbildung 5 sehen.
Abbildung 5:Leistung von Intersections mit temporären Tabellen im Vergleich zu zwei anderen Lösungen
Wie Sie sehen können, schneidet die Lösung mit den temporären Tabellen besser ab als die mit den CTEs, aber sie hat immer noch eine quadratische Skalierung und schneidet im Vergleich zum Cursor sehr schlecht ab.
Was kommt als Nächstes?
Dieser Artikel behandelte den ersten Versuch, die klassische Matching-Aufgabe von Angebot und Nachfrage mithilfe einer mengenbasierten Lösung zu handhaben. Die Idee war, die Daten als Intervalle zu modellieren, Angebot mit Nachfrageeinträgen abzugleichen, indem sich überschneidende Angebots- und Nachfrageintervalle identifiziert wurden, und dann die Handelsmenge basierend auf der Größe der sich überschneidenden Segmente zu berechnen. Sicherlich eine spannende Idee. Das Hauptproblem dabei ist auch das klassische Problem der Identifizierung von Intervallschnittpunkten durch die Verwendung von zwei Bereichsprädikaten. Selbst wenn der beste Index vorhanden ist, können Sie nur ein Bereichsprädikat mit einer Indexsuche unterstützen. das andere Bereichsprädikat muss mit einem Restprädikat behandelt werden. Dies führt zu einem Plan mit quadratischer Komplexität.
Was können Sie also tun, um dieses Hindernis zu überwinden? Es gibt verschiedene Ideen. Eine geniale Idee gehört Joe Obbish, über die Sie in seinem Blogbeitrag ausführlich nachlesen können. Ich werde andere Ideen in den kommenden Artikeln der Serie behandeln.
[ Springe zu:Ursprüngliche Herausforderung | Lösungen:Teil 1 | Teil 2 | Teil 3 ]
